Прямая в пространстве. Решения типовых задач. Часть 3

Решения типовых задач по теме "Задание прямой в пространстве". Часть 3
Задача №1. Установить, лежит ли данная прямая в данной плоскости, параллельна плоскости или пересекает ее:
a)

$$\frac{x-1}{2}=\frac{y+2}{1}=\frac{z-2}{1},\; \; \; 3x-y+2z+5=0;$$

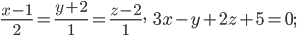
б)

$$\frac{x-2}{-2}=\frac{y-3}{3}=\frac{z-1}{2},\; \; \; 4x+2y+z+24=0;$$

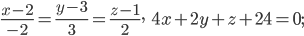
в)

$$\frac{x-2}{-1}=\frac{y+1}{4}=\frac{z+5}{2},\; \; \; 4x+y-z=0.$$

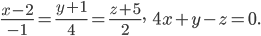
Решение задачи №1 подробно изложено в следующем видео

Задача №2. Составить уравнения прямой, лежащей в пло­скости 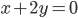$x+2y=0$ и пересекающей прямые

$$\frac{x}{1}=\frac{y}{4}=\frac{z-1}{-1}, \; \; \; \frac{x-4}{2}=\frac{y-1}{0}=\frac{z-2}{-1}$$

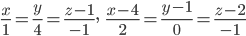
Решение. Если прямая, лежащая в плоскости 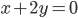$x+2y=0$, пересекает две данные прямые, то и эти пря­мые пересекают данную плоскость в некоторых двух точках, через которые проходит искомая прямая. Поэто­му найдем точки пересечения двух данных прямых с дан­ной плоскостью.
Точка пересечения первой прямой с плоскостью: $x=t,\; y=4t,\; z=-t+1;\; t+8t=0,\; t=0,\; x=0,\; y=0,\; z=1;\; A(0;0;1).$
Точка пересечения второй прямой с плоскостью: $x=2t+4,\; y=1,\; z=-t+2;\; 2t+4+2=0,\; t=-3;$
$x=-6+4=-2,\; y=1,\; z=3+2=5;\; B(-2;1;5).$
Уравнения прямой будем искать по формуле:

$$\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}};$$

$$\frac{x}{-2}=\frac{y}{1}=\frac{z-1}{5-1};\; \frac{x}{-2}=\frac{y}{1}=\frac{z-1}{4}.$$

Ответ: $\frac{x}{-2}=\frac{y}{1}=\frac{z-1}{4}.$


Задача №3. Через начало координат провести плоскость, параллельную к двум пересекающимся прямым
$\frac{x-1}{2}=\frac{y-7}{7}=\frac{z-3}{4},\; \; \; \frac{x-6}{3}=\frac{y+1}{-2}=\frac{z+2}{1}.$
Решения задач №2 и №3 подробно изложены в следующем видео

Задача №4. Составить уравнение плоскости, содержащей пересекающиеся прямые

$$\frac{x}{2}=\frac{y-1,5}{1}=\frac{z-1}{-2},\; \; \frac{x+7}{1}=\frac{y-8}{-2}=\frac{z}{1}.$$

Задача №5. Через точку пересечения плоскости $3x-y-2z-5=0$ с прямой

$$\frac{x-7}{5}=\frac{y-4}{1}=\frac{z-5}{4}$$

провести прямую, лежащую в этой плоскости и перпен­дикулярную к данной прямой.
Решения задач №4 и №5 подробно изложены в следующем видео

Задача №6. Составить уравнения прямой, проходящей через точку пересечения прямой

$$\frac{x-3}{2}=\frac{y+1}{-1}=\frac{z-2}{5}$$

и плоскости $3x-4y+2z-1=0$ и точку М (3;-3;0).
Задача №7. Найти расстояние от точки А (1;3;5) до пря­мой

$$\frac{x+30}{6}=\frac{y-0}{2}=\frac{z+2,5}{-1}.$$

Решения задач №6 и №7 подробно изложены в следующем видео

Задача №8. Вычислить кратчайшее расстояние между дву­мя прямыми:

$$\frac{x-2}{1}=\frac{y+2}{-3}=\frac{z+1}{-2}\; \; \; (1)$$

и

$$\frac{x-0}{1}=\frac{y-0}{1}=\frac{z-1}{1}\; \; \; (2)$$

Задача №9. Найти кратчайшее расстояние между диа­гональю куба и не пересекающей ее диагональю грани, если ребро куба равно 1.
Решения задач №1 и №2 подробно изложены в следующем видео