Общая теория кривых второго порядка
Основной задачей преобразования координат является упрощение уравнения кривой.
Уравнение одной и той же кривой может иметь различный вид в зависимости от того, как будет расположена система осей координат, к которой отнесена кривая. Удачным выбором расположения осей координат можно добиться простейшего вида уравнения кривой.
Общее уравнение кривой второго порядка имеет вид:
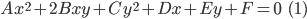
Задача упрощения этого уравнения состоит в том, чтобы в преобразованном уравнении исчезли: член с произведением текущих координат и члены первого измерения.
По упрощенному уравнению легко установить тип кривой и схематически построить эту кривую.
Если в уравнении (1) отсутствует член с произведением координат ху, т. е. уравнение имеет вид:
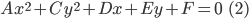
то оно преобразуется к каноническому виду параллельным переносом осей координат по формулам
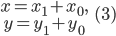
или
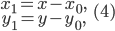
где 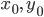 — координаты нового начала О₁ и
— координаты нового начала О₁ и 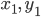 — новые координаты.
— новые координаты.
Цель переноса — уничтожение членов первого измерения. Упрощение выполняется методом выделения полных квадратов. Если в уравнении (1) отсутствуют члены первого измерения, т. е. уравнение имеет вид:
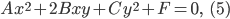
то оно преобразуется к каноническому виду поворотом осей координат по формулам:
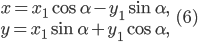
где 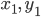 — новые координаты, α — угол поворота.
— новые координаты, α — угол поворота.
Цель этого поворота — уничтожение члена с произведением ко¬ординат в уравнении кривой.
В общем случае, когда уравнение кривой второго порядка содержит член с произведением координат и члены первого измерения, упрощение следует начинать с поворота осей, без изменения начала координат.







