Пример 5. Вычислить работу, необходимую для выкачивания масла из вертикального цилиндрического резервуара высотой  м и радиусом основания
м и радиусом основания  м. Удельный вес масла
м. Удельный вес масла  .
.
Решение. Величина работы 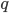 , затрачиваемой на поднятие некоторого тела, зависит от высоты
, затрачиваемой на поднятие некоторого тела, зависит от высоты  его подъема:
его подъема:  ,
, 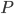 — вес тела.
— вес тела.
Допустим, что работа, затраченная на выкачивание из резервуара слоя масла толщиною  , рис. 1, есть некоторая функция
, рис. 1, есть некоторая функция  и найдем дифференциал этой функции.
и найдем дифференциал этой функции.
При увеличении  на величину
на величину  объем
объем  слоя масла увеличится на величину
слоя масла увеличится на величину  , его вес
, его вес  увеличится на величину
увеличится на величину  , а затраченная работа
, а затраченная работа 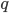 увеличится на величину
увеличится на величину  .
.
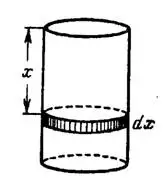
Рис. 1
Всю искомую работу  получим при изменении
получим при изменении  от 0 до
от 0 до 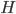 . Поэтому
. Поэтому
 (кГм)
(кГм) 
 (дж)
(дж)  (дж).
(дж).
Пример 6. При условиях предыдущей задачи вычислить работу, необходимую для выкачивания масла из цилиндрического резервуара, если его ось имеет горизонтальное направление.
Решение. Как и в решении предыдущей задачи, полагаем, что работа, затрачиваемая на выкачивание из резервуара слоя масла толщиною  (рис. 2), есть некоторая функция
(рис. 2), есть некоторая функция  и найдем дифференциал этой функции.
и найдем дифференциал этой функции.
При увеличении  на величину
на величину  объем
объем  слоя масла увеличится на величину
слоя масла увеличится на величину  , его вес
, его вес  увеличится на величину
увеличится на величину  , а затраченная работа
, а затраченная работа 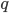 увеличится на величину
увеличится на величину  .
.
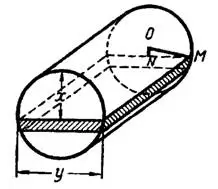
Рис. 2
Вся искомая работа  выразится интегралом от
выразится интегралом от  в пределах от
в пределах от  до
до  :
:

где переменная  выражена через переменную
выражена через переменную  из прямоугольного треугольника
из прямоугольного треугольника  .
.
Для вычисления этого интеграла полагаем  . Тогда
. Тогда  при
при  при
при  ;
;
 (кГм)
(кГм)  (дж).
(дж).
Пример 7. Шар лежит на дне бассейна глубиной  дм. Определить работу, необходимую для извлечения шара из воды, если его радиус
дм. Определить работу, необходимую для извлечения шара из воды, если его радиус  дм, а удельный вес
дм, а удельный вес  .
.
Решение. При подъеме шара до поверхности воды сила  , совершающая работу, постоянна и равна разности между весом шара и весом вытесняемой им воды:
, совершающая работу, постоянна и равна разности между весом шара и весом вытесняемой им воды:

Поэтому работа  необходимая для поднятия шара до поверхности воды, определяется элементарным путем как произведение силы
необходимая для поднятия шара до поверхности воды, определяется элементарным путем как произведение силы  на высоту подъема
на высоту подъема  :
:

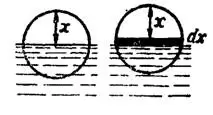
Рис. 3
При дальнейшем подъеме шара сила  , совершающая работу, будет изменяться в зависимости от высоты
, совершающая работу, будет изменяться в зависимости от высоты  надводной части шара (рис. 3):
надводной части шара (рис. 3):

где  — вес шара,
— вес шара,  — вес воды, вытесняемой подводной частью шара, численно равный объему шарового сегмента с высотой
— вес воды, вытесняемой подводной частью шара, численно равный объему шарового сегмента с высотой  :
:

Очевидно, и работа, совершаемая силой  , будет некоторой функцией
, будет некоторой функцией  . Допуская, что при подъеме шара еще на малую высоту
. Допуская, что при подъеме шара еще на малую высоту  сила
сила  остается неизменной, найдем приближенную величину приращения работы
остается неизменной, найдем приближенную величину приращения работы
![\displaystyle \Delta q\approx p(x)dx=(P_{sh}-p_{v})dx=\frac{\pi }{3}[4R^{3}(\delta -1)-x^{3}+3Rx^{2}]dx=dq.](https://math-helper.ru/wp-content/plugins/latex/cache/tex_c126aba45739511acfcabd2a08b7b7c8.gif)
Интегрируя  в пределах от
в пределах от  до
до  , найдем работу
, найдем работу  , которую надо совершить, чтобы шар, поднятый со дна бассейна до поверхности воды, полностью извлечь из воды:
, которую надо совершить, чтобы шар, поднятый со дна бассейна до поверхности воды, полностью извлечь из воды:
![\displaystyle Q_{2}=\frac{\pi }{3}\int_{0}^{2R}[4R^{3}(\delta -1)-x^{3}+3Rx^{2}]dx=\frac{\pi }{3}\left [ 4R^{3}(\delta -1)x-\frac{x^{4}}{4}+Rx^{3} \right ] \left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{2R}=\frac{4}{3}\pi R^{4}(2\delta -1).](https://math-helper.ru/wp-content/plugins/latex/cache/tex_66fdaf4134640fa63ec7f03534cadd65.gif)
Вся искомая работа
![\displaystyle Q=Q_{1}+Q_{2}=\frac{4}{3}\pi R^{3}[R+(\delta -1)H]=61,2\pi](https://math-helper.ru/wp-content/plugins/latex/cache/tex_a2f2d7726933abdb474c39651a76fdea.gif) (кГм)
(кГм) (дж).
(дж).







