Пример 8. Определить работу, необходимую для запуска ракеты весом  с поверхности земли на высоту
с поверхности земли на высоту  км.
км.
Решение. Сила 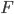 притяжения тела землей или вес тела зависит от его расстояния
притяжения тела землей или вес тела зависит от его расстояния  до центра земли:
до центра земли:  , где
, где 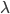 — постоянная.
— постоянная.
Если 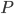 есть вес тела, когда оно находится на поверхности земли, т. е. на расстоянии земного радиуса
есть вес тела, когда оно находится на поверхности земли, т. е. на расстоянии земного радиуса 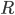 от центра земли, то
от центра земли, то  и сила
и сила 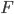 , преодолеваемая двигателем поднимающейся ракеты в момент, когда она находится на расстоянии
, преодолеваемая двигателем поднимающейся ракеты в момент, когда она находится на расстоянии  от центра земли, является известной функцией от
от центра земли, является известной функцией от  :
:

Полагая, что работа, совершаемая двигателем ракеты при подъеме ее на высоту  , есть некоторая функция
, есть некоторая функция  и допуская, что при дальнейшем подъеме ракеты на малую высоту
и допуская, что при дальнейшем подъеме ракеты на малую высоту  сила
сила 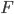 остается неизменной, найдем приближенную величину приращения работы
остается неизменной, найдем приближенную величину приращения работы

При подъеме ракеты с поверхности земли на высоту 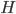 переменная
переменная  изменяется от
изменяется от 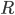 до
до  . Поэтому искомая работа
. Поэтому искомая работа  выражается интегралом
выражается интегралом

При  км,
км,  км,
км,  кГм
кГм  дж.
дж.
Работу, которую должен совершить двигатель, чтобы полностью освободить ракету от земного притяжения, можно определить как предел работы  при неограниченном возрастании
при неограниченном возрастании 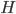 :
:
![\displaystyle \underset{H \to \infty }{lim}Q(H)=\underset{H \to \infty }{lim}\frac{PRH}{R+H}=\underset{H \to \infty } {lim}\left [ PR:\left ( \frac{R}{H}+1 \right )\right ]=PR.](https://math-helper.ru/wp-content/plugins/latex/cache/tex_e4dfa33887fbc23c2894196d6d37a434.gif)
При указанных значениях 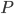 и
и 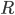 эта работа составит 9 600 000 000 кГм
эта работа составит 9 600 000 000 кГм  94176 000 000 дж.
94176 000 000 дж.
Пример 9. Цилиндр высотой  м и радиусом
м и радиусом  м, наполненный газом под атмосферным давлением (10330 кг/м²), закрыт поршнем. Определить работу, затрачиваемую на изотермическое сжатие газа при перемещении поршня на расстояние
м, наполненный газом под атмосферным давлением (10330 кг/м²), закрыт поршнем. Определить работу, затрачиваемую на изотермическое сжатие газа при перемещении поршня на расстояние  м внутрь цилиндра.
м внутрь цилиндра.
Решение. При изотермическом изменении состояния газа, когда его температура остается неизменной, зависимость между объемом  и давлением
и давлением  газа выражается формулой
газа выражается формулой  . (Закон Бойля — Мариотта.)
. (Закон Бойля — Мариотта.)
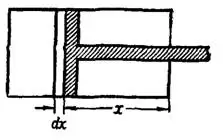
Рис. 1
Поэтому, если поршень будет вдвинут на  м внутрь цилиндра (рис. 1), то давление
м внутрь цилиндра (рис. 1), то давление  газа на единицу площади поршня будет
газа на единицу площади поршня будет  , а давление на всю площадь
, а давление на всю площадь 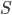 поршня будет
поршня будет 
Полагая, что работа, затрачиваемая при в движении поршня на  м, есть некоторая функция
м, есть некоторая функция  , и допуская, что при дальнейшем в движении поршня на малое расстояние
, и допуская, что при дальнейшем в движении поршня на малое расстояние  испытываемое им давление
испытываемое им давление  остается неизменным, найдем приближенную величину приращения (дифференциал) функции
остается неизменным, найдем приближенную величину приращения (дифференциал) функции  :
:

Всей искомой работе  соответствует изменение
соответствует изменение  от 0 до
от 0 до 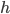 , поэтому
, поэтому

При  м,
м,  м,
м,  м,
м,  кг/м², найдем
кг/м², найдем  м³;
м³;  кГм
кГм  дж.
дж.
Пример 10. При условиях предыдущей задачи определить работу адиабатического сжатия газа, при котором его объем  и давление
и давление  связаны соотношением
связаны соотношением  (закон Пуассона), где
(закон Пуассона), где 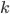 — постоянная для данного газа величина, большая единицы. (Для воздуха
— постоянная для данного газа величина, большая единицы. (Для воздуха  .)
.)
Решение. Повторяя те же рассуждения и употребляя те же обозначения, как и в решении предыдущей задачи, найдем следующее выражение для дифференциала работы:

Интегрируя в пределах от  до
до  получим всю искомую работу
получим всю искомую работу
![\displaystyle Q=\frac{c}{S^{k-1}}\int_{0}^{h}\frac{dx}{(H-x)^{k}}=\frac{c}{S^{k-1}}\int_{h}^{0}(H-x)^{-k}d(H-x)=\frac{c}{S^{k-1}}\frac{(H-x)^{1-k}}{1-k} \left.\begin{matrix} \\ \\ \end{matrix}\right| _{h}^{0}=\frac{p_{0}v_{0}^{k}}{S^{k-1}(k-1)}\left [ \frac{1}{(H-h)^{k-1}}-\frac{1}{H^{k-1}} \right ]=\frac{p_{0}v_{0}}{k-1}\left [ \left ( \frac{H}{H-h} \right )^{k-1}-1 \right ].](https://math-helper.ru/wp-content/plugins/latex/cache/tex_9c2da0995f3a9d03b7dbadc8e207b6e0.gif)
Полагая  м,
м,  , найдем
, найдем ![\displaystyle Q\approx \frac{2479,2\pi }{0,4}\left [ \left ( \frac{1,5}{0,3} \right )^{0,4}-1 \right ]\approx 17593,4](https://math-helper.ru/wp-content/plugins/latex/cache/tex_74c85526a1d181972c8895a46ab459db.gif) кГм
кГм  дж.
дж.
Сравнение этого результата с предыдущими показывает, что работа, затрачиваемая при адиабатическом сжатии газа, больше, чем при изотермическом.







