Проекции вектора

1. Проекции вектора. Проекцией вектора 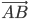$\vec{AB}$ на ось 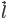$\vec{l}$ называется число, равное длине отрезка 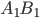$A_{1}B_{1}$ взятое со знаком плюс, если направление отрезка 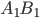$A_{1}B_{1}$ совпадает с направлением оси 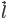$\vec{l}$, и со знаком минус, если эти направления противоположны (рис.1).

Проекция вектора 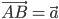$\vec{AB}=\vec{a}$ на ось 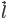$\vec{l}$ обозначается формулой
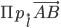$\Pi p_{\vec{l}}\vec{AB}$ или $\Pi p_{\vec{l}}\vec{a}.$
Проекция вектора 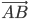$\vec{AB}$ на ось 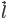$\vec{l}$ выражается формулой

$$\Pi p_{\vec{l}}\vec{AB}=AB\cos \phi$$

или $\Pi p_{\vec{l}}\vec{a}=a\cos \phi$,
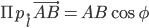
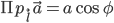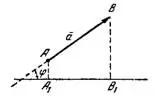
где АВ = а — модуль вектора 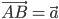$\vec{AB}=\vec{a}$, φ — угол наклона вектора к оси $\vec{l}$.
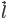Проекция суммы векторов на ось 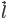$\vec{l}$ равна сумме их проекций на ту же ось: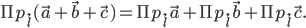

$$\Pi p_{\vec{l}}(\vec{a}+\vec{b}+\vec{c})=\Pi p_{\vec{l}}\vec{a}+\Pi p_{\vec{l}}\vec{b}+\Pi p_{\vec{l}}\vec{c}.$$

При умножении вектора на скаляр его проекция умножается на этот скаляр:

$$\Pi p_{\vec{l}}n\vec{a}=n\Pi p_{\vec{l}}\vec{a}.$$

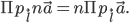
Рассмотрим прямоугольную систему координат и произвольный вектор 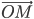$\vec{OM}$ (рис.2).
Очевидно, будем иметь:
$\vec{OM}=\vec{OM_{1}}+\vec{OM_{2}}+\vec{OM_{3}},$
или иначе.

$$\vec{M}=\vec{M_{1}}+\vec{M_{2}}+\vec{M_{3}},\; \; \; \left(1 \right)$$

где

$$\vec{OM}=\vec{M},\; \vec{OM_{1}}=\vec{M_{1}},\; \vec{OM_{2}}=\vec{M_{2}},\; \vec{OM_{3}}=\vec{M_{3}}.$$

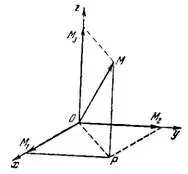
Равенство (1) показывает, что всякий вектор можно разложить на три слагаемых вектора, лежащик на осях координат. Слагаемые векторы $\vec{M_{1}}$, $\vec{M_{2}}$ и $\vec{M_{3}}$ называются составляющими вектора \vec{M} относительно системы осей координат Oxyz или его компонентами.
От точки О в положительном направлении каждой оси координат откладываем вектор, длина которого равна 1. Эти векторы называются единичными векторами или ортами и обозначаются соответственно через $\vec{i}$, $\vec{j}$ и $\vec{k}$ (рис.3).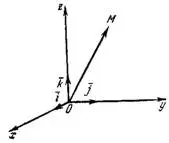

Возвращаясь к равенству (1), заметим, что вектор $\vec{M_{1}}$ как и вектор $\vec{i}$, расположены на оси_абсцисс, а потому имеем $\vec{M_{1}}=x\vec{i}$, где х есть длина вектора $\vec{M_{1}}$, взятая со знаком плюс, если направления векторов $\vec{M_{1}}$ и $\vec{i}$ совпадают, и со знаком минус, если направления их противоположны. 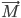Другими словами, х есть число, являющееся проекцией вектора $\vec{M}$ на ось абсцисс.
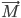Аналогично получим:$\vec{M_{2}}=y\vec{j}$ и $\vec{M_{3}}=z\vec{k}$, где у и z — проекции вектора $\vec{M}$ соответственно на оси ординат и аппликат.
Тогда равенство (1) перепишется так:

$$\vec{M}=x\vec{i}+y\vec{j}+z\vec{k}.\; \; \; (2)$$

Равенство (2) дает разложение вектора по основным единичным векторам или по ортам $\vec{i}$, $\vec{j}$ и $\vec{k}$.
Вместо полной записи $\vec{M}=x\vec{i}+y\vec{j}+z\vec{k}$ часто пользуются сокращенной $\vec{M}=\left\{x,y,z \right\}$ или $\vec{M}\left\{x,y,z \right\}$.
Здесь х, у, z обозначают проекции вектора 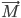$\vec{M}$, или координаты точки М, являющейся концом радиуса-вектора $\vec{M}$.
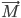Длина вектора 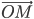$\vec{OM}$ определяется по формуле:

$$OM=\sqrt{x^{2}+y^{2}+z^{2}}.\; \; \; \left(3 \right)$$

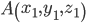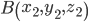Если даны две точки $A\left(x_{1},y_{1},z_{1} \right)$ и $B\left(x_{2},y_{2},z_{2} \right)$, являющиеся соответственно началом и концом вектора $\vec{a}=\vec{AB}$, то его проекции на оси координат соответственно равны:

$$x=x_{2}-x_{1},\; y=y_{2}-y_{1},\; z=z_{2}-z_{1},$$

а сам вектор в этом случае может быть записан в виде:

$$\vec{a}=\vec{AB}=\left(x_{2}-x_{1} \right)\vec{i}+\left(y_{2}-y_{1} \right)\vec{j}+\left(z_{2}-z_{1} \right)\vec{k}.\;$$

Его длина определяется по формуле:

$$a=\sqrt{\left(x_{2}-x_{1} \right)^{2}+\left(y_{2}-y_{1} \right)^{2}+\left(z_{2}-z_{1} \right)^{2}}.\; \; \; \left(4 \right)$$

Обозначив через α, β и γ углы вектора $\vec{a}$ с осями координат, получим:

$$\cos \alpha =\frac{x_{2}-x_{1}}{a},\; \cos \beta =\frac{y_{2}-y_{1}}{a},\; \cos \gamma =\frac{z_{2}-z_{1}}{a},\; \; \; \left(5 \right)$$

$\cos \alpha ,\; \cos \beta ,\; \cos \gamma$ называются направляющими косинусами вектора $\vec{a}$.
Из формул (4) и (5) следует:

$$\cos \alpha =\frac{x_{2}-x_{1}}{\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}},$$

$$\cos \beta =\frac{y_{2}-y_{1}}{\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}},\;\;\;(6)$$

$$\cos \gamma =\frac{z_{2}-z_{1}}{\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}}.$$

2. Действия над векторами, заданными своими проекциями.
а) При сложении векторов одноименные их проекции складываются. Если даны векторы

$$\vec{a}=x_{1}\vec{i}+y_{1}\vec{j}+z_{1}\vec{k},\; \vec{b}=x_{2}\vec{i}+y_{2}\vec{j}+z_{2}\vec{k}$$

то

$$\vec{a}+\vec{b}=\left(x_{1}+x_{2} \right)\vec{i}+\left(y_{1}+y_{2} \right)\vec{j}+\left(z_{1}+z_{2} \right)\vec{k}.$$

б) При вычитании векторов одноименные их проекции вычитаются:

$$\vec{a}-\vec{b}=\left(x_{1}-x_{2} \right)\vec{i}+\left(y_{1}-y_{2} \right)\vec{j}+\left(z_{1}-z_{2} \right)\vec{k}.$$

в) При умножении вектора на скаляр проекции вектора умножаются на этот скаляр:

$$\vec{a}\lambda =\lambda x_{1}\vec{i}+\lambda y_{1}\vec{j}+\lambda z_{1}\vec{k}$$

Равенство (2) устанавливает связь между геометрической и алгебраической частями теории векторов.