Скалярным произведением двух векторов называется число (скаляр), равное произведению их длин, умноженному на косинус угла между ними (рис.1).
Скалярное произведение обозначается одним из трех способов
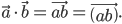
Если угол между векторами
 и
и  обозначить через φ, то согласно определению имеем:
обозначить через φ, то согласно определению имеем: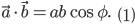
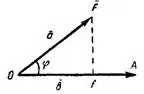
Рис.1
Из формулы (1) следует, что скалярное произведение векторов  и
и  можно выразить также формулами:
можно выразить также формулами:
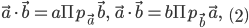
т. е. скалярное произведение двух векторов равно длине одного из них, умноженной на проекцию другого вектора на направление первого.
Из формулы (1) следует также, что:
а) Если
 и
и  ненулевые векторы, то cкалярное произведение равно нулю только в том случае, если
ненулевые векторы, то cкалярное произведение равно нулю только в том случае, если  и
и  перпендикулярны.
перпендикулярны.б) Если φ — острый угол, то
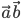 >0.
>0.в) Если φ — тупой угол, то
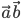 <0.
г) Скалярное произведение обладает свойством коммутативности (переместительности):
<0.
г) Скалярное произведение обладает свойством коммутативности (переместительности):
 .
д) Скалярное произведение обладает свойством распределительности
.
д) Скалярное произведение обладает свойством распределительности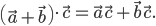
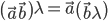
Если векторы
 и
и  заданы своими проекциями:
заданы своими проекциями: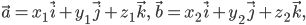
то скалярное произведение этих векторов равно сумме произведений их одноименных проекций:
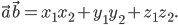
При
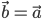 имеем
имеем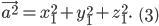
С другой стороны
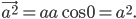
Тогда
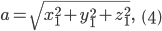
т. е. длина вектора равна корню квадратному из суммы квадратов его проекций.
Угол между двумя векторами. Из формулы (1) следует:
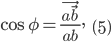
или в координатной форме:
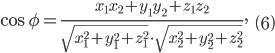
т. е. косинус угла между векторами равен их скалярному произведению, деленному на произведение их длин.
Направляющие косинусы вектора
 с осями координат выражаются так:
с осями координат выражаются так:







