Основные понятия и формулы по теме "Прямая и плоскость в пространстве".
1. Угол между прямой
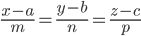
и плоскостью
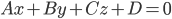
определяется по формуле:
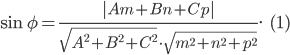
2. Условие параллельности прямой и плоскости имеет вид:
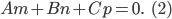
3. Условие перпендикулярности прямой и плоскости имеет вид:
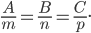
4. Если даны две плоскости
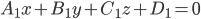 и
и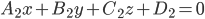 , то уравнение всякой плоскости, проходящей через линию пересечения заданных плоскостей, имеет вид:
, то уравнение всякой плоскости, проходящей через линию пересечения заданных плоскостей, имеет вид: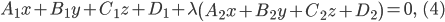
где
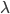 — переменный параметр.
— переменный параметр.Уравнение (4) называется уравнением пучка плоскостей.
5. Условием, при котором две прямые

и

лежат в одной плоскости, является равенство

Если условие (5) выполняется, то прямые лежат в одной плоскости, т. е. они или параллельны, если направляющие коэффициенты пропорциональны, или пересекаются, если направляющие коэффициенты не пропорциональны.
Если же условие (5) не выполняется, то прямые скрещиваются.
6. Условием, при котором прямая
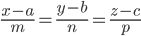
лежит в плоскости
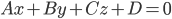 , являются следующие равенства:
, являются следующие равенства:







