Прямая в пространстве. Решения типовых задач. Часть 1

Решения типовых задач по теме "Задание прямой в пространстве". Часть 1
Задача №1. Построить прямую, заданную общими уравне­ниями

$$\left\{\begin{matrix} x+3y+3z-6=0,\\ 3x+3y+4z-10=0. \end{matrix}\right.$$

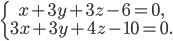
Построение. Так как две данные плоскости, не параллельные между собой (не выполня­ется условие параллельности двух плоскостей), то в пе­ресечении они дают прямую.
Построим каждую из данных плоскостей. Первая плоскость на осях координат отсекает отрезки а = 6, b = 2, c = 2. Вторая плоскость отсекает отрезки

$$a_{1}=3\frac{1}{3},\; b_{1}=3\frac{1}{3},\; c=2\frac{1}{2}.$$

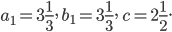
Линия MN пересечения данных плоскостей и есть ис­комая прямая.
Задача №2. Как расположены следующие прямые:
а)

$$\left\{\begin{matrix} x+y-z+2=0,\\ 3x-1=0; \end{matrix}\right.$$

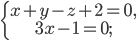
б)

$$\left\{\begin{matrix} 2x-3=0,\\ y+5=0; \end{matrix}\right.$$

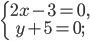
в)

$$\left\{\begin{matrix} x-y+2z=0,\\ 2x+3y-z=0; \end{matrix}\right.$$

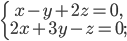
г)

$$\left\{\begin{matrix} 3x+5y-6=0,\\ x-2y+3=0; \end{matrix}\right.$$

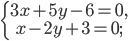
д)

$$\left\{\begin{matrix} y+2z=0,\\ 3y-z=0; \end{matrix}\right.$$

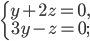
е)

$$\left\{\begin{matrix} 2y+z=0,\\ 3x-1=0; \end{matrix}\right.$$

ж)

$$\left\{\begin{matrix} x-2y+5z-4=0,\\ x-4y+5z-4=0; \end{matrix}\right.$$

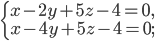
Решения задач №1 и №2 подробно изложены в следующем видео

Задача №3. Составить канонические и параметрические уравнения прямой, проходящей через точку М(1;2;3), если направляющий вектор 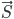$\vec{S}$ прямой образует с коор­динатными осями Ох, Оу, Oz углы соответственно

$$\alpha =\frac{2}{3}\pi ,\; \beta =\frac{\pi }{3},\; \gamma =\frac{\pi }{4}.$$

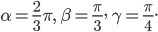
Задача №4. Привести к каноническому виду уравнения пря­мой

$$\left\{\begin{matrix} x-2y+3z-4=0,\\ 3x+2y-5z-4=0. \end{matrix}\right.$$

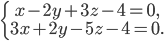
Решения задач №3 и №4 подробно изложены в следующем видео

Задача №5. Привести общие уравнения прямой

$$\left\{\begin{matrix} x-3y+2z+4=0,\\ 2x+y-3z-6=0. \end{matrix}\right.$$

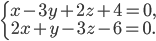
к уравнениям в проекциях на координатные плоскости xOz и yOz.
Задача №6. Найти уравнение проекции прямой

$$\frac{x-1}{9}=\frac{y+1}{-4}=\frac{z-0}{-7}$$

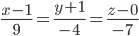
на плоскость Р, заданную уравнением

$$2x-y-3z+6=0$$

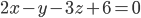
Решения задач №3 и №4 подробно изложены в следующем видео