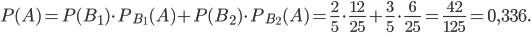Задача №1. В урну, содержащую 3 шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все варианты предположений о первоначальном составе шаров (по цвету).
Решение. Рассмотрим следующие предположения о первоначальном составе шаров (гипотезы):
 - в урне было 3 белых шара;
- в урне было 3 белых шара;
 - в урне были 2 белых шара и 1 шар другого цвета;
- в урне были 2 белых шара и 1 шар другого цвета;
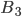 - в урне были 1 белый шар и 2 шара другого цвета;
- в урне были 1 белый шар и 2 шара другого цвета;
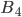 - в урне не было белых шаров.
- в урне не было белых шаров.
Обозначим событие:  - извлечен белый шар.
- извлечен белый шар.
Гипотезы (i = 1; 2; 3; 4) составляют полную группу несовместных событий; сумма вероятностей этих событий равна единице: 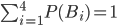 .
.
Поскольку имеется 4 гипотезы, причем по условию они равновероятны, то вероятность каждой гипотезы равна 1/4, т. е. 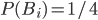 .
.
Событие  может произойти только с одним из событий
может произойти только с одним из событий 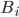 . Так как в урну добавляют один белый шар, то условные вероятности события
. Так как в урну добавляют один белый шар, то условные вероятности события  равны:
равны:
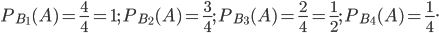
Искомую вероятность того, что извлеченный шар окажется белым, найдем по формуле полной вероятности (1) при n = 4:
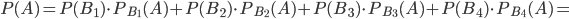
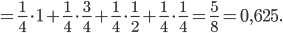
Задача №2. В трех урнах находятся белые и черные шары: в первой - 2 белых и 3 черных, во второй - 2 белых и 2 черных, в третьей - 3 белых и 1 черный. Из первой урны переложили шар во вторую. После этого шар из второй урны переложили в третью. Наконец, из третьей урны шар переложили в первую. Чему равна вероятность того, что состав шаров во всех урнах не изменился?
Решение. Испытание состоит в перекладывании шара из одной урны в другую. После трех испытаний состав шаров в урнах не изменится в том случае, если во всех испытаниях брать шар одного и того же цвета. Рассмотрим события:
 - после трех испытаний состав шаров в урнах не изменился;
- после трех испытаний состав шаров в урнах не изменился; - из урны I в урну II переложен белый шар;
- из урны I в урну II переложен белый шар; - из урны I в урну II переложен черный шар.
- из урны I в урну II переложен черный шар.Вероятность гипотезы
 равна
равна 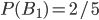 , вероятность гипотезы
, вероятность гипотезы  равна
равна 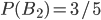 .
.Возможны следующие два несовместные варианта наступления события
 :
:1) событие
 наступает вместе с событием
наступает вместе с событием  ;
;2) событие
 наступает вместе с событием
наступает вместе с событием  .
.Рассмотрим первый вариант. После того, как из урны I взяли белый шар и положили в урну II, в урне II стало 3 белых и 2 черных шара. После того, как из урны II взяли белый шар и положили в урну III, в урне III стало 4 белых шара, и 1 черный шар. Событие
 произойдет, если совместно наступят два такие события:
произойдет, если совместно наступят два такие события: - из урны II взят белый шар и положен в урну III;
- из урны II взят белый шар и положен в урну III;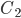 - из урны III взят белый шар и положен в урну I.
- из урны III взят белый шар и положен в урну I.Вероятность
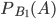 найдем по теореме умножения вероятностей зависимых событий:
найдем по теореме умножения вероятностей зависимых событий: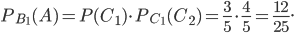
Рассмотрим второй вариант. После того, как из урны I взяли черный шар и положили в урну II, в урне II стало 2 белых и 3 черных шара. После того, как из урны II взяли черный шар и положили в урну III, в урне III стало 3 белых и 2 черных шара. Событие
 произойдет, если совместно наступят два такие события:
произойдет, если совместно наступят два такие события: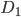 - из урны II взят черный шар и положен в урну III;
- из урны II взят черный шар и положен в урну III;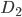 - из урны III взят черный шар и положен в урну I.
- из урны III взят черный шар и положен в урну I.Вероятность
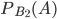 найдем по теореме умножения вероятностей зависимых событий:
найдем по теореме умножения вероятностей зависимых событий: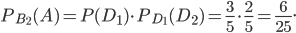
Вероятность события
 найдем по формуле (1):
найдем по формуле (1):