Решение задач на классическое определение вероятности. Часть 5

Задача №1. В зрительном зале забронировано 10 мест для приглашенных гос­тей. Пришли 7 приглашенных. Найти вероятность того, что четверо из пришедших гостей займут определенные для каждого из них места, если гости занимают места случайным образом.
Решение. Обозначим событие: А - А пришедших гостя займут определенные для каждого из них места.
Вероятность события А найдем по формуле (1). Числа m и n, входящие в эту формулу, получим, воспользовавшись формулами теории со­единений.
Имеется 10 элементов - 10 забронированных в зрительном зале мест. Эти элементы представлены на рис.1, они помечены номерами от 1 до 10. На рис.1 показан один из возможных вариантов размещения 7-ми человек на 10-ти забронированных местах. Свободные места изображены символами $\bigcirc$; места, занятые четырьмя гостями из семи пришедших изображены символами $\bullet$, а занятые остальными тремя из семи пришедших - симво­лами $\oplus$.

Общее число n исходов испытания найдем, исходя из следующего рассуждения. Всего имеется 10 элементов (10 забронированных мест в за­ле). Составляют соединения, в каждое из которых входят 7 элементов (7 занимаемых пришедшими гостями мест). Соединения отличаются друг от друга как самими элементами, так и порядком этих элементов; в рассмат­риваемом случае порядок элементов существенен для подсчета различных вариантов соединений. Следовательно, рассматриваемые соединения представляют собой размещения из 10 элементов по 7. По формуле (3) полу­чим: $n=A_{10}^{7}=10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4.$
Число m исходов испытания, благоприятствующих событию А, най­дем, принимая во внимание следующее. Если 4 человека занимают опреде­ленные для каждого из них места (например, на места 4,5,6,7, как это пока­зано на рис.1), (то есть сядут на забронированные для них места и при этом в определенном порядке), то оставшиеся 3 человека могут занимать осталь­ные 6 мест. Итак, составляем соединения из 6-ти элементов, в каждое из этих соединений входят 3 элемента. Соединения отличаются друг от друга как самими элементами, так и их порядком; в рассматриваемом случае порядок элементов важен для подсчета различных вариантов соединений. Следовательно, рассматриваемые соединения представляют собой размещения из шести элементов по три. По формуле (3) получим: $m=A_{6}^{3}=6\cdot 5\cdot 4.$
Искомая вероятность события А равна

$$P(A)=\frac{m}{n}=\frac{A_{6}^{3}}{A_{10}^{7}}=\frac{6\cdot 5\cdot 4}{10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4}=\frac{1}{5040}.$$

Задача №2. Шифры книг в библиотечном каталоге состоят из шести цифр и не начинаются с цифры 0. Читатель отыскивает в каталоге шифр нужной ему книги. Какова вероятность того, что все цифры шифра окажутся различными?
Решение. Обозначим событие: А - все цифры отыскиваемого читате­лем шифра различны. Найдем вероятность события А, применив формулу (1).
Определим числа m и n, входящие в эту формулу.
Всего имеется десять элементов - десять цифр: о, 1,..., 9. В шифре книги цифрами заняты 1-е, 2-е,..., 6-е места, которым присвоим номера I,II,III,...,VI.
Существует десять вариантов занять место I цифрами 0,1,...,9 и по десять таких же вариантов занять остальные места II - VI. Каждый их деся­ти вариантов занять место I может быть соединен с любым из десяти вари­антов занять места II - VI, поэтому общее число исходов испытания $n=10^{6}$.
Возможны следующие варианты занять шесть мест различными цифрами: 2-5-6-9-8-7, 2-6-5-9-8-7, 0-4-6-7-5-3 , 1-4-6-7-5-3 и дру­гие (часть из них представляет собой соединения цифр, начинающиеся с цифры 0). Эти варианты, число которых равно 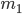$m_{1}$ являются соедине­ниями, в каждое из которых входят 6 элементов из имеющихся 10-ти. Со­единения отличаются друг от друга как самими элементами, так и поряд­ком элементов (порядок элементов важен). Следовательно, рассматри­ваемые соединения представляют собой размещения из десяти элементов по шесть: $m_{1}=A_{10}^{6}$
По условию, шифр не начинается с цифры 0. Поэтому из числа 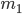$m_{1}$ вариантов соединений с различными цифрами нужно исключить число $m_{2}$ вариантов соединений, имеющих различные цифры и начинающихся с ну­ля. Если считать, что место I занято цифрой 0, то остальные пять мест за­полняются различными цифрами из оставшихся девяти; следовательно, $m_{2}=A_{9}^{5}$.
Таким образом,

$$m=m_{1}-m_{2}=A_{10}^{6}-A_{9}^{5}=10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5-9\cdot 8\cdot 7\cdot 6\cdot 5=136080.$$

Вероятность события А равна $P(A)=\frac{m}{n}=\frac{136080}{10^{6}}=0,13608.$


Задача №3. На столе лежат две стопки тетрадей. В первой стопке - 5 тетрадей в синей обложке, во второй - 5 тетрадей в красной обложке. Тетради каж­дой из этих стопок пронумерованы цифрами 1, 2, 3, 4, 5 и расположены в случайном порядке номеров. Студент берет из каждой стопки по одной тетради. Найти вероятность того, что студент возьмет из обеих стопок тетради с номером 5 при обязательном выполнении условий:
а) будет извлечена тетрадь №5 в синей обложке;
б) будет извлечена хотя бы одна тетрадь №5;
в) будут извлечены две тетради с одинаковыми номерами.
Решение. Испытание состоит в извлечении двух тетрадей из сто­пок. Составим квадратную матрицу пятого порядка, характеризующую все 25 равновозможных исходов этого испытания, представляющих собой полную группу несовместных событий:

$$D=\begin{pmatrix} 11 & 12 & 13 &14 &15 \\ 21 & 22 & 23 & 24 & 25\\ 31 &32 & 33 &34 &35 \\ 41 & 42 & 43 & 44 &45 \\ 51 & 52 & 53 &54 & 55 \end{pmatrix}$$

Элементами матрицы D являются двузначные числа. Первая цифра в каждом из этих чисел - номер тетради в синей обложке, а вторая - номер тетради в красной обложке. Рассмотрим события:
А - извлечение тетрадей под номером 5 из обеих стопок при условии, что обязательно будет извлечена тетрадь №5 в синей обложке;
В - извлечение тетрадей под номером 5 из обеих стопок при условии, что обязательно будет извлечена хотя бы одна тетрадь №5;
С - извлечение тетрадей под номером 5 из обеих стопок при условии, что обязательно будут извлечены две тетради с одинаковыми померши.
Вероятности событий A, B и C найдем по формуле (1). Благоприят­ствующим событию А (а также событиям В и С) исходом является ис­ход, представленный в матрице D элементом 55; таким образом, m = 1.
Общее число возможных исходов для событий А, В и С будет раз­личным.
а) Возможные исходы испытания для события А представлены в мат­рице D элементами ее последней строки: 51,52,53,54,55. Таким образом, общее число всех равновозможных исходов, образующих полную группу несовместных событий, равно n.
Вероятность события n, согласно формуле (1), равна Р(А) = 1/5.
б) Возможные исходы испытания для события В представлены в мат­рице D числами, coдеpжaщими цифру 5: 15, 25, 35, 45, 51, 52, 53, 54, 55. Общее число всех равновозможных несовместных исходов испытания, об­разующих полную группу, равно n
Вероятность события В, согласно формуле (1), равна Р(В) = 1/9.
в) Возможные исходы испытания для события С представлены в мат­рице D числами, состоящими из двух одинаковых цифр: 11,22, 33,44, 55. Общее число всех равновозможных несовместных исходов испытания, об­разующих полную группу, равно n = 5.
По формуле (1) получим Р(С) = 1/5.