Решение задач на уравнение касательной прямой и нормальной плоскости. Практикум по математическому анализу. Урок 42

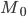Если $x=x(t),y=y(t),z=z(t)$ — параметрические уравнения кривой и $M_{0}(x_{0},y_{0},z_{0})$ - точка этой кривой, то касательная прямая к этой кривой в точке $M_{0}$ определяется уравнениями
$\displaystyle \frac{x-x_{0}}{\dot{x_{0}}}=\frac{y-y_{0}}{\dot{y_{0}}}=\frac{z-z_{0}}{\dot{z_{0}}}\; \; \; \; (1)$
а нормальная плоскость (перпендикулярная к касательной) определяется уравнением
$\displaystyle (x-x_{0})\dot{x_{0}}+(y-y_{0})\dot{y_{0}}+(z-z_{0})\dot{z_{0}}=0\; \; \; \; (2)$
Пример 1. Найти уравнения касательной прямой и нормальной плоскости к кривой:
1) $\displaystyle x=t^{3},y=t^{2},z=t$ в точке, где $t=-1$;
2) $\displaystyle x=y^{2},y=z^{2}$ в точке, где $z=2$.
Решение. 1) Определяем координаты точки касания: $x=-1,y=1,z=-1$ (подставляя $t=-1$ в данные уравнения). Находим производные от $x,y$ и $z$ по $t$ и вычисляем их значения в точке касания: $\displaystyle \dot{x}=3t^{2},\dot{y}=2t,\dot{z}=1;\dot{x}(-1)=3,\dot{y}(-1)=-2,\dot{z}(-1)=1.$

Подставляя в общие уравнения (1) и (2) координаты точки касания и вычисленные значения производных, получим уравнения касательной прямой $\displaystyle \frac{x+1}{3}=\frac{y-1}{-2}=\frac{z+1}{1}$ и уравнение нормальной плоскости $\displaystyle 3(x+1)-2(y-1)+z+1=0$ или $\displaystyle 3x-2y+z+6=0$.

2) Здесь кривая определена как пересечение двух поверхностей. Вначале преобразуем уравнения кривой к параметрическому виду. Полагая $z=t$, получим $\displaystyle y=t^{2},x=t^{4}$.
Далее определяем координаты точки касания: $x=16,y=4,z=2$ и значения производных $\dot{x},\dot{y},\dot{z}$ в этой точке: $\dot{x}=4t^{3},\dot{y}=2t,\dot{z}=1;\dot{x}(2)=32,\dot{y}(2)=4,\dot{z}(2)=1.$
Подставляя в общие уравнения (1) и (2), получим уравнения касательной

$$\displaystyle \frac{x-16}{32}=\frac{y-4}{4}=\frac{z-2}{1}$$

и уравнение нормальной плоскости
$\displaystyle 32(x-16)+4(y-4)+z-2=0$ или $\displaystyle 32x+4y+z-530=0$.

Пример 2. Найти уравнения касательной к винтовой линии $\displaystyle y=a\cos t,y=a\sin t,z=bt$ в точке, где $\displaystyle t=t_{0}$ и угол, образуемый ею с осью $Oz$.
Решение. Обозначив координаты точки касания $(x_{0},y_{0},z_{0})$ и пользуясь общими уравнениями (1), получим следующие уравнения касательной:

$$\displaystyle \frac{x-x_{0}}{-a\sin t_{0}}=\frac{y-y_{0}}{a\cos t_{0}}=\frac{z-z_{0}}{b}.$$

Отсюда направляющий косинус угла, образованного касательной с осью $Oz$:

$$\displaystyle \cos \gamma =\frac{\dot{z}}{\sqrt{x^{2}+y^{2}+z^{2}}}=\frac{b}{\sqrt{a^{2}\sin ^{2}t_{0}+a^{2}\cos ^{2}t_{0}+b^{2}}}=\frac{b}{\sqrt{a^{2}+b^{2}}}.$$

Этот результат показывает, что все касательные к винтовой линии образуют с осью $Oz$ один и тот же угол.