Вектор-функция скалярного аргумента и ее дифференцирование. Касательная к пространственной кривой. Математический анализ. Урок 41

Переменный вектор $\vec{r}$ называется вектор-функцией скалярного аргумента $t$, если каждому рассматриваемому числовому значению $t$ соответствует определенное значение $\vec{r}$ (т. е. определенный модуль и определенное направление вектора $\vec{r}$).

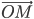Если начало переменного вектора $\vec{r}=\vec{r}(t)$ неизменно помещается в начале координат $O$, т. е. если $\vec{r}(t)$ есть радиус-вектор $\vec{OM}$, то при изменении скаляра $t$ его подвижный конец $M$ описывает некоторую линию, которая называется годографом этого вектора.

При разложении радиуса-вектора $\vec{r}(t)$ по ортам $\vec{r}=x\vec{i}+y\vec{j}+z\vec{k}$ его проекции $r_{x}=x(t),\: r_{y}=y(t),\: r_{z}=z(t)$ совпадают с координатами его конца $M(x,y,z)$, а система $x=x(t),y=y(t),z=z(t)$ представляет параметрические уравнения его годографа.
Производной вектор-функции $\vec{r}(t)$ называется предел $\displaystyle \underset{\Delta t \to 0}{lim}\frac{\overrightarrow{\Delta r}}{\Delta t}$; она обозначается $\displaystyle \frac{\overline{dr}}{dt}$, или $\dot{\vec{r}}$, или $\vec{r'}$.
Правила дифференцирования (нахождения производной) вектор-функции $\vec{r}(t)$ аналогичны правилам дифференцирования скалярных функций:
$\vec{c'}=0$, если $c$ — постоянный вектор.
$(\vec{r_{1}}\pm \vec{r_{2}})'=\vec{r'_{1}}\pm \vec{r'_{2}},\: (\vec{r}u)'=\vec{r'}u+\vec{r}u'.$
Если $\vec{r}=x\vec{i}+y\vec{j}+z\vec{k}$, то $\dot{\vec{r}}=\dot{x}\vec{i}+\dot{y}\vec{j}+\dot{z}\vec{k}$. Вектор $\dot{\vec{r}}$ направлен по касательной к годографу вектора $\vec{r}$.
Если вектор $\vec{r}(t)$ изменяется только по направлению, то его годограф представляет линию, расположенную на сфере радиуса $R=\left | \vec{r} \right |$ с центром в начале координат, а вектор $\dot{\vec{r}}$ перпендикулярен к годографу вектора $\dot{\vec{r}}$, если вектор $\vec{r}(t)$ изменяется только по модулю, то его годограф представляет луч, исходящий из начала координат, а вектор $\dot{\vec{r}}$ направлен по этому лучу.

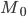Всякую кривую можно рассматривать как годограф радиуса-вектора ее текущей точки $M(x,y,z)$. Поэтому, если $x=x(t),y=y(t),z=z(t)$ — параметрические уравнения кривой и $M_{0}(x_{0},y_{0},z_{0})$ - точка этой кривой, то касательная прямая к этой кривой в точке $M_{0}$ определяется уравнениями

$$\displaystyle \frac{x-x_{0}}{\dot{x_{0}}}=\frac{y-y_{0}}{\dot{y_{0}}}=\frac{z-z_{0}}{\dot{z_{0}}}\; \; \; \; (1)$$

а нормальная плоскость (перпендикулярная к касательной) определяется уравнением

$$\displaystyle (x-x_{0})\dot{x_{0}}+(y-y_{0})\dot{y_{0}}+(z-z_{0})\dot{z_{0}}=0\; \; \; \; (2)$$