Скорость и ускорение криволинейного движения. Практикум по математическому анализу. Урок 43

Если в любой момент времени $t$ положение движущейся точки $M$ определяется ее радиусом-вектором $\overrightarrow{OM}=\vec{r}(t)$, то $\dot{\vec{r}}$ есть вектор скорости, $\ddot{\vec{r}}$ есть вектор ускорения, а годограф вектора $\vec{r}$ есть траектория движения точки $M$.
Вектор скорости $\overrightarrow{OM}=\vec{r}(t)$ направлен по касательной к траектории, а его модуль равен производной от пути по времени $\displaystyle \left |\dot{\vec{r}} \right |=\frac{ds}{dt}$.
Пример 1. Зная уравнение движения точки, определить (назвать), какую линию представляет ее траектория и найти скорость и ускорение этой точки:
1) $\displaystyle \vec{r}=(3t-2)\vec{i}-4t\vec{j};$ 2) $\displaystyle \vec{r}=2\cos t\cdot \vec{i}+\sin t\cdot \vec{k};$
3) $\displaystyle \vec{r}=(2t^{2}-3)\vec{i}-3t^{2}\vec{j}+(4t^{2}-5)\vec{k};$
4) $\displaystyle \vec{r}=a\sin \omega t\cdot \vec{i}+a\cos \omega t\cdot \vec{j}+bt\vec{k}$.
Решение. 1) Траектория точки есть годограф ее радиуса-вектора $\displaystyle \vec{r}\left \{ 3t-2;-4t \right \}$, т. е. линия, определяемая параметрическими уравнениями $\displaystyle x=3t-2,y=-4t$. Исключая из них параметр (время) $t$, получим прямую $\displaystyle 4x+3y+8=0$, расположенную в плоскости $xOy$.
Скорость $\displaystyle \vec{v}$ и ускорение $\displaystyle \vec{w}$ движения точки найдем как первую и вторую производные от $\displaystyle \vec{r}$ по $t$:

$$\displaystyle \vec{v}=\dot{\vec{r}}=3\vec{i}-4\vec{j};\vec{\omega }=\ddot{\vec{r}}=0.$$

Следовательно, точка движется прямолинейно с постоянной скоростью, модуль которой $\displaystyle \left |\vec{v} \right |=\sqrt{3^{2}+(-4)^{2}}=5.$
2) Здесь траектория точки есть эллипс, определяемый параметрическими уравнениями $\displaystyle x=2\cos t,z=\sin t$ или уравнением $\displaystyle \frac{x^{2}}{4}+z^{2}=1$, который расположен в плоскости $xOz$.
Скорость точки $\displaystyle \vec{v}=\dot{\vec{r}}=-2\sin t\cdot \vec{i}+\cos t\cdot \vec{k}$ ускорение $\displaystyle \vec{w}=\ddot{\vec{r}}=-2\cos t\cdot \vec{i}-\sin t\cdot \vec{k}.$
3) Параметрические уравнения траектории точки $\displaystyle x=2t^{2}-3,y=-3t^{2},z=4t^{2}-5$ после исключения параметра $t$ преобразуются в канонические уравнения прямой $\displaystyle \frac{x+3}{2}=\frac{y}{-3}=\frac{z+5}{4}.$
Скорость точки $\displaystyle \vec{v}=\dot{\vec{r}}=4t\vec{i}-6t\vec{j}+8t\vec{k},$ ускорение $\displaystyle \vec{w}=\ddot{\vec{r}}=4\vec{i}-6\vec{j}+8\vec{k}$ - постоянно (не зависит от времени $t$).
Здесь движение точки является прямолинейным и равномерно-переменным.
4) Траектория точки есть цилиндрическая винтовая линия $\displaystyle x=a\sin \omega t,y=a\cos \omega t,z=bt.$
Скорость точки $\displaystyle \vec{v}=\dot{\vec{r}}=a\omega \cos \omega t\cdot \vec{i}-a\omega \sin \omega t\cdot \vec{j}+b\vec{k},$
ускорение $\displaystyle \vec{w}=\ddot{\vec{r}}=-a\omega^{2} \sin \omega t\cdot \vec{i}-a\omega^{2} \cos \omega t\cdot \vec{j}.$
Здесь движение точки является равномерным, так как модуль скорости $\displaystyle \left | \vec{v} \right |=\sqrt{a^{2}\omega ^{2}+b^{2}}$ остается неизменным.
Пример 2. Зная уравнение движения точки $\displaystyle \vec{r}=\cos^{3}t\cdot \vec{i}+\sin^{3}t\cdot \vec{j}$ построить ее траекторию и векторы скорости и ускорения в моменты времени $\displaystyle t_{1}=\frac{\pi }{6}$ и $\displaystyle t_{2}=\frac{\pi }{4}$.

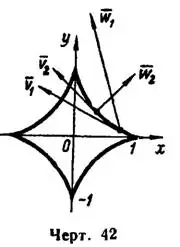
Решение. Траектория точки или годограф вектора $\displaystyle \vec{r}$ есть астроида $\displaystyle x=\cos ^{3}t,y=\sin ^{3}t.$
В любой момент времени $t$ скорость точки $\displaystyle \vec{v}=\dot{\vec{r}}=-3\cos ^{2}t\sin t\cdot \vec{i}+3\sin ^{2}t\cos t\cdot \vec{j}$, а ее ускорение $\displaystyle \vec{w}=\ddot{\vec{r}}=3\cos t(3\sin ^{2}t-1)\vec{i}+3\sin t(3\cos ^{2}t-1)\vec{j}.$
В момент $\displaystyle t_{1}=\frac{\pi }{6},\: \vec{v}_{1}=-\frac{9}{8}\vec{i}+\frac{3\sqrt{3}}{8}\vec{j},\vec{w}_{1}=-\frac{3\sqrt{3}}{8}\vec{i}+\frac{15}{8}\vec{j}.$
В момент $\displaystyle t_{2}=\frac{\pi }{4},\: \vec{v}_{2}=\frac{3}{2\sqrt{2}}(\vec{j}-\vec{i}),\vec{w}_{2}=\frac{3}{2\sqrt{2}}(\vec{i}+\vec{j}).$
Траектория точки и найденные векторы ее скорости и ускорения в моменты $\displaystyle t_{1}=\frac{\pi }{6}$ и $\displaystyle t_{2}=\frac{\pi }{4}$ построены на черт. 42.