Решения типовых задач по теме: "Скалярное произведение векторов"
Задача № 1. Векторы  и
и  образуют угол
образуют угол 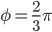 . Зная,
. Зная,
что 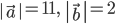 , вычислить:
, вычислить:
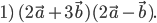
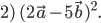
Решение. Так как скалярное произведение двух векторов равно произведению их длин, умноженному на косинус угла между ними, и скалярный квадрат вектора равен квадрату его длины, будем иметь:
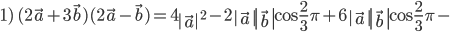
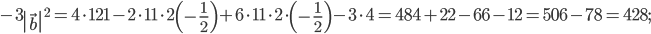
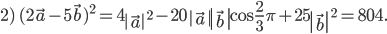
Ответ: 1) 428; 2) 804.
Задача № 2. Определить, при каком значении  векторы
векторы 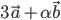 и
и 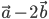 будут взаимно перпендикулярными, если
будут взаимно перпендикулярными, если 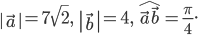
Решения этих задач подробно изложено в следующем видео
Задача № 3. Вычислить тупой угол, образованный медианами, проведенными из вершин острых углов равнобедренного прямоугольного треугольника.
Задача № 4. Зная одну из вершин треугольника А (1; —6; - 3) и векторы, совпадающие с двумя его сторонами 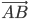 {0; 3; 5} и
{0; 3; 5} и  {4; 2; —1}, найти остальные вершины и сторону
{4; 2; —1}, найти остальные вершины и сторону  .
.
Решение. Найдем координаты вершины В, исходя из формул, что проекции вектора равны:

Откуда

Таким образом,

В( 1; -3; 2).
Аналогично найдем координаты точки С:

С(5; -1; 1).
Теперь найдем вектор
 :
:
Ответ: B(1; -3; 2), С(5; -1; 1),
 {—4; -5; -4}.
{—4; -5; -4}.Решения этих задач подробно изложено в следующем видео
Задача № 5. В плоскости yOz найти вектор 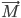 , перпендикулярный вектору
, перпендикулярный вектору 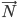 {12;-3;4} и имеющий одинаковую с ним длину.
{12;-3;4} и имеющий одинаковую с ним длину.
Задача № 6. Вычислить, какую работу производит сила  {6; - 2; 1}, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения А(3;4;—2) в положение В (4;-2;-3).
{6; - 2; 1}, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения А(3;4;—2) в положение В (4;-2;-3).
Решение. Найдем проекции вектора 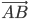 , по которому перемещается точка приложения силы
, по которому перемещается точка приложения силы  , по фомулам
, по фомулам

т. е.

Следовательно, имеем
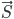 =
=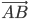 {1;-6;-1}.
{1;-6;-1}.Так как работа численно равна скалярному произведению производящей ее силы на пройденный путь, то найдем скалярное произведение векторов
 и
и 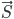 :
:
Ответ: А = 17 (единиц работы).
Решения этих задач подробно изложено в следующем видео
Задача № 7. Дан треугольник с вершинами А (- 2; 3; 1), В (-2; -1; 4) и С (- 2; -4; 0). Определить его внутренний угол при вершине С.
Задача № 8. Даны три вектора  { 1; —4; 8},
{ 1; —4; 8},  {4; 4: -2},
{4; 4: -2}, 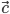 {2; 3; 6}.
{2; 3; 6}.
Вычислить проекцию вектора  на вектор
на вектор  .
.
Решения этих задач подробно изложено в следующем видео







