Решения типовых задач по теме: "Векторное произведение векторов"
Задача № 1. Даны модули векторов  и
и  ,
, 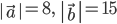 , и их скалярное произведение
, и их скалярное произведение  Вычислить модуль векторного произведения
Вычислить модуль векторного произведения ![\left|[\vec{a}\vec{b}] \right|](https://math-helper.ru/wp-content/plugins/latex/cache/tex_f249c38881fd0b4543a84754e053cd06.gif) .
.
Решение. Так как модуль векторного произведения двух векторов равен произведению модулей данных векторов, умноженному на синус угла между векторами, то необходимо знать синус угла между векторами  и
и  .
.
Воспользуемся скалярным произведением данных векторов:
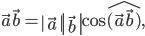
откуда
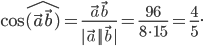
Тогда
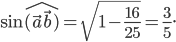
Следовательно,
![\left|[\vec{a}\vec{b}] \right|=\left|\vec{a} \right|\left|\vec{b} \right|\sin \hat{(\vec{a}\vec{b})}=8\cdot 15\cdot \frac{3}{5}=72.](https://math-helper.ru/wp-content/plugins/latex/cache/tex_f0cfdd50fcb0a08fea4d18a1a805f1e9.gif)
Ответ:
![\left|[\vec{a}\vec{b}] \right|=72.](https://math-helper.ru/wp-content/plugins/latex/cache/tex_328ddf47a23f165a6ecb77cb06b604cf.gif)
Задача № 2. Какому условию должны удовлетворять векторы
 и
и  , чтобы векторы
, чтобы векторы 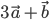 и
и 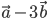 были коллинеарны?
были коллинеарны?Решения этих задач подробно изложено в следующем видео
Задача № 3. Векторы  ,
,  и
и 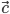 удовлетворяют условию
удовлетворяют условию  . Доказать, что
. Доказать, что ![\left[\vec{a}\vec{b} \right]=\left[\vec{c} \vec{a}\right]=\left[\vec{b}\vec{c} \right]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_22a319595c467df8c07a7dfb32e680e6.gif) .
.
Задача № 4. Вычислить площадь параллелограмма, построенного на векторах  и
и  , если
, если и
и 
Указания. Площадь параллелограмма численно равна длине вектора, полученного в результате векторного умножения двух данных векторов, т. е.

Ответ: S параллелограмма= 157,5 кв. ед.
Решения этих задач подробно изложено в следующем видео
Задача № 5. Зная стороны треугольника 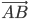 ={-3; -2; 6} и
={-3; -2; 6} и  = {- 2; 4; 4}, вычислить длину высоты
= {- 2; 4; 4}, вычислить длину высоты  .
.
Решение. I способ приведен в видеоуроке
II способ. Указания. Найти Пр и затем по теореме Пифагора вычислить высоту
и затем по теореме Пифагора вычислить высоту  .
.
Ответ:  ед. длины.
ед. длины.
Решение этой задачи подробно изложено в следующем видео
Задача № 6. Решить самостоятельно. Вычислить длины диагоналей и площадь параллелограмма, построенного на векторах:  {6;0;2} и
{6;0;2} и  {1,5; 2; 1}.
{1,5; 2; 1}.
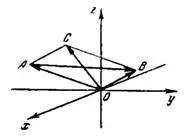
Указания. Одна из диагоналей параллелограмма будет равна сумме векторов сторон, а другая — разности векторов сторон параллелограмма (рис.1).

Ответ: длины диагоналей
 и
и  , площадь параллелограмма 13 кв.ед.
, площадь параллелограмма 13 кв.ед.Задача № 7. Зная, что векторы
 и
и  коллинеарны, вычислить коэффициенты α и β.
коллинеарны, вычислить коэффициенты α и β.Указания. Если векторы а и b коллинеарны, то их векторное произведение равно нулю,
 .
.Ответ:

Решения этих задач подробно изложено в следующем видео







