Пример 2. При  найти пределы следующих функций:
найти пределы следующих функций:
1) 
2) 
3) 
Решение. Каждая из данных функций представляет сумму  членов арифметической прогрессии. Разность первой прогрессии
членов арифметической прогрессии. Разность первой прогрессии  , второй
, второй  и третьей
и третьей  .
.
Выполняя сложение и переходя к пределу, найдем:
1) 

2) 

3) 
![\displaystyle \underset{n \to +\infty }{\textrm{lim}}S_{3}=\frac{1}{2}\left [\frac{1}{\textrm{lim}\: n}-\frac{1}{(\textrm{lim}\: n)^{2}} \right ]=0.](https://math-helper.ru/wp-content/plugins/latex/cache/tex_d361e367880cb6487eaf053dcd13ffa1.gif)
В этой задаче, при  функции
функции  и
и  являются суммами бесконечно малых величин, число которых неограниченно возрастает вместе с
являются суммами бесконечно малых величин, число которых неограниченно возрастает вместе с  . Полученные результаты показывают, что
. Полученные результаты показывают, что 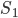 есть величина бесконечно большая,
есть величина бесконечно большая, 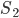 — величина, стремящаяся к
— величина, стремящаяся к  ,
,  — величина бесконечно малая.
— величина бесконечно малая.
Следовательно, решение этой задачи показывает: если число слагаемых бесконечно малых неограниченно возрастает, их сумма может оказаться любой величиной.
Пример 3. Доказать, что  при любом значении
при любом значении  .
.
Решение. Каково бы ни было значение  , всегда найдутся такие два последовательных целых положительных числа
, всегда найдутся такие два последовательных целых положительных числа 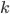 и
и  , между которыми заключается
, между которыми заключается  , т. е.
, т. е.  . Исходя из этого, получим очевидное неравенство:
. Исходя из этого, получим очевидное неравенство:

Первый множитель  не зависит от
не зависит от  и при любом данном значении
и при любом данном значении  является постоянным; второй множитель
является постоянным; второй множитель  при
при  будет величиной бесконечно малой, ибо
будет величиной бесконечно малой, ибо  . (См. решение задачи 2 (урок 10).)
. (См. решение задачи 2 (урок 10).)
Поэтому  , как произведение постоянной величины на бесконечно малую, есть величина бесконечно малая. Вследствие этого функция
, как произведение постоянной величины на бесконечно малую, есть величина бесконечно малая. Вследствие этого функция  также будет величиной бесконечно малой, т. е.
также будет величиной бесконечно малой, т. е.  при любом значении
при любом значении  .
.







