Пусть U — столь обширное множество, что все рассматриваемые множества окажутся его подмножествами.
U — универсальное множество (иначе оно называется основное множество). Универсальным множеством для элементарной арифметики является, например, множество Z — множество всех целых чисел; для аналитической геометрии универсальное множество есть R — множество всех действительных чисел (числовая прямая), а также R² — множество упорядоченных пар (числовая плоскость).
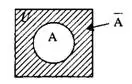Дополнением множества А (обозначение Ā или сА) называется множество элементов универсального множества U, не принадлежащих множеству А.
Ā={x|xͼU, xɇA}. (1)
Если U изобразить в виде прямоугольника, то множество заштриховано на рис.
Основные свойства операции дополнения
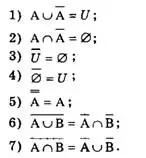
Свойства 6) и 7) называют правилами де Моргана.
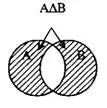
Симметрической разностью (обозначение АΔВ) множеств А и В называется множество элементов, которые принадлежат только множеству А или только множеству В.
АΔВ={x| xͼA и xɇB} или АΔВ={x| xͼB и xɇA} (2)
Иначе можно записать:
АΔВ=(A/B)U(b/A) (2а)
На рис. 2 симметрическая разность АΔВ заштрихована.
