Операции над множествами

Пересечением (или произведением) множеств А и В (обозначение А∩В или А•В) называется множество, состоящее из элементов, принадлежащих одновременно как множеству А, так и множеству B:
А∩В={x|xͼA и xͼB} (1)
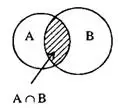Название «пересечение» происходит от того, что при пересечении множеств точек двух геометрических фигур получают множество точек пересечения этих фигур в самом обычном смысле слова. Так, если множества А и В интерпретировать, например, как круги, то А∩В — общая часть этих кругов. На рис. 4 множество А∩В заштриховано.
Замечание. Схематическое изображение множеств, когда множества изображаются в виде кругов или каких-нибудь других простых областей, называется диаграммами Венна (иногда этот способ изображения множеств называют кругами Эйлера).
Пример 1. A = [-1;1], В = (0;3). А∩В = (0;1].
Если множества А и В не пересекаются, то их пересечение — пустое множество. Таким образом, для непересекающихся множеств А∩В = Ǿ.
Пример 2. А = (1;3), В = (4;5) . А∩В = Ǿ.
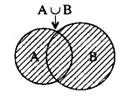Объединением (или суммой) множеств А и В (обозначение АUВ или А+В) называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств.
А∩В={x|xͼA или xͼB} (2)
На рис. множество АUВ заштриховано.
Пример З. А = {1;5;9}, В = {2;3;9} , АUВ = {1;2;3;5;9}.
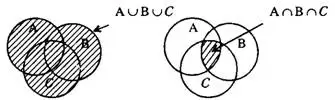
Иногда приходится рассматривать пересечение и объединение трех и более множеств. Например, объединение множеств А, В, С есть множество, каждый элемент которого принадлежит хотя бы одному из множеств — А, В или С (см. рис.3). Пересечение множеств А, В, С есть множество всех элементов, принадлежащих и множеству А, и множеству В, и множеству С (рис. 4).

Рис. 3 Рис. 4

Основные свойства операций объединения и пересечения множеств
Операции объединения и пересечения обладают следующими свойствами
1) АUВ = ВUА;
2) А∩В = В∩А;
3) (АUВ)UC = АU(ВUГ);
4) (A∩B)∩C = A∩(B∩C);
5) (АUВ)∩C = (A∩C)U(B∩C);
6) A∩(BUC) = (A∩B)U(A∩C);
7) AU(B∩C) = (AUB)∩(AUC);
8) (AUC)∩(BUC) =(A∩B)UC;
9) AUA = A;
10) AUA = A;
11) AnǾ = Ǿ;
12) AUǾ= A.

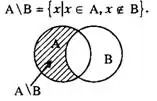
Разностью множеств (обозначение A\B) называется множество, состоящее из элементов, которые принадлежат множеству А, но не принадлежат множеству В. На рис.5 множество А\В заштриховано.