Каждому значению х є D(f) равенство у = f(x) ставит вполне определенное значение у є E(f). В некоторых случаях равенство у = f(x) можно рассматривать как такое, которое каждому значению у є E(f) ставит в соответствие вполне определенное значение х є D(f).
Пример 1. Равенство у=3х—1 каждому значению у ставит в соответствие х=(у+1)/3. Можно сказать, что равенство у=3х—1 определяет х как некоторую функцию переменной у, т. е х=(у+1)/3.
Пусть функция у = f(x) такова, что по каждому допустимому значению величины у можно восстановить одно и только одно значение величины х. Тогда это равенство определяет х как не которую функцию от у. Обозначим эту функцию через φ: х=φ(у) В этом соотношении х=ф(у) роль аргумента играет у, а роль функции — х. Поскольку обычно х обозначает аргумент, у обозначает функцию, то перепишем зависимость х=φ(у) в виде у=φ(х). Функция у=φ(х) называется обратной по отношению к функции у=f(x).
Так, например, у=3х—1<=> х=(у+1)/3. Поэтому функция у=(х+1)/3 является обратной к функции у=Зх-1.
Для того чтобы у функции у = f(x) при х є [a;b] существовала обратная к ней функция, необходимо и достаточно, чтобы функция у = f(x) была монотонной при х є [a;b] (то есть или только возрастающей, или только убывающей).
Так, для функции у = х³ обратной является
![]()
х є (-∞;∞). Для функции у = х² при х є (-∞;+∞) обратной не существует, однако при х є (0;∞) обратной для у = х² является y=√x, а при х є (-∞;0) обратной для у = х² является функция y=-√x.
Если точка (х;у) принадлежит графику функции у = f(x), то точка (у;х) принадлежит графику обратной функции. Поэтому графики прямой и обратной функции симметричны друг другу относительно прямой у=х(биссектрисы 1-го и 3-го координатных углов).
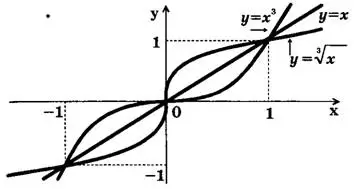
Так, например, график функции у= х³ симметричен графику функции
![]()
относительно прямой у = х (см. рис.). Вообще для функции
![]()
обратной является
![]()
Замечание. Область определения обратной функции совпадает с множеством значений исходной функции, а множество значений обратной функции совпадает с областью определения исходной функции, т. е. область определения и область значений прямой и обратной функций меняются местами.
Обратная функция






