Примеры решения неравенств с модулем

Примеры решения неравенств с модулем
Пример 5. Решить неравенство $\left | 2x-4 \right |<x-1.$

Решение.
1 способ. Исходное неравенство можно заменить совокупностью двух систем:

$\left\{\begin{matrix} 2x-4\geq 0,\\ 2x-4<x-1; \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2x-4<0,\\ -(2x-4)<x-1. \end{matrix}\right.$

Из первой системы получаем

$2\leq x<3$ из второй системы —

$\frac{5}{3}\leq x<2$ . Искомое решение будет объединением решений первой и второй систем, т. е.

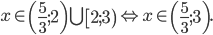
$x\in \left ( \frac{5}{3};2 \right ) \bigcup \left [ 2;3 \right )\Leftrightarrow x\in \left ( \frac{5}{3};3 \right ).$
2 способ.

$\left | 2x-4 \right |<x-1 \Leftrightarrow -\left ( x-1 \right )<2x-4<x-1\Leftrightarrow -x+1<2x-4<x-1\Leftrightarrow$

$\Leftrightarrow \left\{\begin{matrix} 2x-4>-x+1,\\ 2x-4<x-1 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3x>5,\\ x<3 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x>\frac{5}{3},\\ x<3. \end{matrix}\right.$

Ответ:

$x\in \left ( \frac{5}{3};3 \right ).$
Пример 6. Решить неравенство

$x^{2}>\left | 5x+6 \right |.$
Решение. Поскольку

$\left | 5x+6 \right |=\left\{\begin{matrix} 5x+6,\; x\geq -\frac{6}{5}\\ -5x-6,\; x<-\frac{6}{5} \end{matrix}\right.$ то исходное неравенство можно заменить совокупностью двух систем неравенств:

$a)\; \left\{\begin{matrix} x\geq -\frac{6}{5},\\ x^{2}>5x+6; \end{matrix}\right.\; \; b)\; \left\{\begin{matrix} x<-\frac{6}{5},\\ x^{2}>-5x-6. \end{matrix}\right.$

Решим эти две системы неравенств а) и b):

$a)\; \left\{\begin{matrix} x\geq -\frac{6}{5},\\ x^{2}-5x-6>0; \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq -\frac{6}{5},\\ x<-1;\: x>6; \end{matrix}\right.\Leftrightarrow -\frac{6}{5}\leq x<-1;\; x>6.$

$a)\; \left\{\begin{matrix} x< -\frac{6}{5},\\ x^{2}+5x+6>0; \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x< -\frac{6}{5},\\ x<-3;\: x>-2; \end{matrix}\right.\Leftrightarrow x<-3;\; -2<x<-\frac{6}{5}.$