Пример 7. Решить неравенство  Решение. При решении исходного неравенства используем метод интервалов для модулей. Отметим на числовой прямой точки, в которых выражения, находящиеся под знаками модулей, обращаются в нуль. Это точки
Решение. При решении исходного неравенства используем метод интервалов для модулей. Отметим на числовой прямой точки, в которых выражения, находящиеся под знаками модулей, обращаются в нуль. Это точки 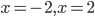 . Вся числовая прямая разбивается этими точками на три интервала (три промежутка):
. Вся числовая прямая разбивается этими точками на три интервала (три промежутка): 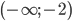 (1 интервал),
(1 интервал), ![\left [ -2;2 \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_da85c62bd00df449a7324d734b297171.gif) (2 интервал),
(2 интервал), 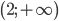 (3 интервал). Приведем две формы записи решения исходного неравенства.
(3 интервал). Приведем две формы записи решения исходного неравенства.
1 форма записи решения.
На 1 интервале 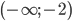 по определению модуля имеем
по определению модуля имеем

Значит, на 1 интервале исходное неравенство равносильно такому:
Так как рассматривается интервал
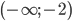 , то в множество решений входит пересечение множеств:
, то в множество решений входит пересечение множеств:  — решение исходного неравенства на 1 интервале.
— решение исходного неравенства на 1 интервале.На отрезке
![\left [ -2;2 \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_da85c62bd00df449a7324d734b297171.gif) (2 интервал)
(2 интервал)
и мы имеем
 , т. е. верное числовое неравенство. Поэтому все значения переменной, принадлежащие этому отрезку, входят в множество решений, т. е.
, т. е. верное числовое неравенство. Поэтому все значения переменной, принадлежащие этому отрезку, входят в множество решений, т. е. ![x\in \left [ -2;2 \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_d2f915daceed9ae8ffd5e75fe8d7362c.gif) — решение на 2 интервале.
На 3 интервале
— решение на 2 интервале.
На 3 интервале 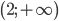
 , и мы получаем
, и мы получаем  . Поскольку рассматривается интервал
. Поскольку рассматривается интервал  , то в множество решений входит пересечение множеств
, то в множество решений входит пересечение множеств  — решение на 3 интервале.
Объединяя полученные результаты, делаем вывод: исходное неравенство выполняется при
— решение на 3 интервале.
Объединяя полученные результаты, делаем вывод: исходное неравенство выполняется при![x\in \left ( -3;-2 \right )\bigcup \left [ -2;2 \right ]\bigcup \left ( 2;3 \right )=\left ( -3;3 \right ).](https://math-helper.ru/wp-content/plugins/latex/cache/tex_ea5538a5f707bc5a8a33da210f5ab8d1.gif)
 — решение исходного неравенства. Ответ:
— решение исходного неравенства. Ответ:  .
.2 форма записи решения. Рассмотрим три случая:
![2)\: \left\{\begin{matrix} -2\leq x\leq 2,\\ x+2-(x-2)<6 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -2\leq x\leq 2,\\ 4<6 \end{matrix}\right.\Leftrightarrow x\in \left [ -2;2 \right ];](https://math-helper.ru/wp-content/plugins/latex/cache/tex_87fbfb8652416f69c006c61460269a1c.gif)
Объединяя найденные множества значений
 , получаем
, получаем![x\in (-3;-2)\bigcup \left [ -2;2 \right ]\bigcup (2;3)=(-3;3).](https://math-helper.ru/wp-content/plugins/latex/cache/tex_d996216b4025774cbde5f99df260d233.gif)

Пример 8. Решить неравенство .
Решение.
Сделав замену переменной
 получаем
получаемВозвращаясь к старой переменной, получаем, что исходное неравенство эквивалентно следующему:
Ответ:







