Степень действительного числа с рациональным показателем
Если
![]()
то полагают по определению
![]()
Например,
![]()
Замечание. Формула
![]()
имеет смысл не только при а > 0. Если n=2k+1 (k ∈ N)то эта формула справедлива
при a∈R\{0}. Если m/n>0, то выражение
![]()
имеет смысл не только при а>0, но и при а ≤ 0, причем
![]()
Например, имеют смысл следующие выражения, которые можно записать с помощью радикалов:
![]()
![]()
Степень действительного числа с действительным показателем
Степень действительного числа с действительным показателем обладает теми же свойствами, что и степень с натуральным, целым, рациональным показателями. Запишем эти свойства, предполагая, что а>0, b>0, хєR, yєR.
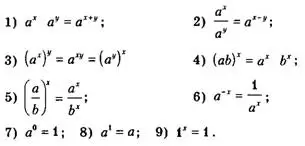
Пример.
![]()
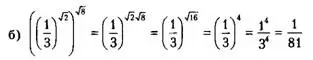
Замечание 1. Выражение aˣ обычно рассматривается при а>0, т. к. при а>0 выражение aˣ имеет смысл всегда. Однако при а а) для неотрицательных целых x≥0;
б) для рациональных чисел
![]()
у которых знаменатель q — нечетное число;
в) когда х — целое отрицательное число.
Например, выражения
![]()
существуют (имеют смысл); выражения
![]()
не существуют в области действительных чисел.
Замечание 2. Обычно переменные обозначаются буквами х, У, z, и, v, w, а постоянные (или параметры) — буквами а, Ь, с, α, β, γ и т. д. Если основание степени обозначить через х, а показатель степени через α, то степень принимает вид хᵅ. Так как преобразования со степенями вида хᵅ встречаются довольно часто, то запишем свойства степени 1)—9), условно назвав их свойствами степени с переменным основанием и фиксированным показателем степени (x>0, у>0, αєR, βєR).
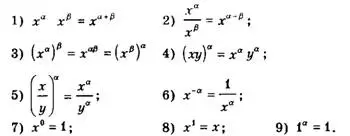
Замечание 3. Выражение хᵅ обычно рассматривают при х>0, т. к. при х>0 хᵅ имеет смысл всегда. Однако при α>0 (α — целое) хᵅ определено для любого х є R; если α — целое отрицательное число, то хᵅ определено при xє R\{0}; если
![]()
где q — нечетное число, то хᵅ определено не только при х>0, но и при х<0.






