Вынесение множителя из-под корня
Если показатель степени множителя под корнем больше, чем показатель корня, то рациональный множитель можно вынести из-под знака корня:
![]()
Пример. Вынести множитель из-под корня:
![]()
Решение.
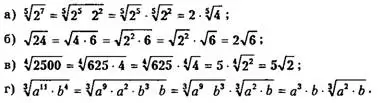
Ответ:
![]()
Внесение множителя под корень
Если рациональный множитель стоит перед корнем, то его можно внести под корень. Для этого нужно этот множитель возвести в степень корня:
![]()
если a≥0, b≥0
Для корней четной степени в зависимости от знака а имеем:
![]()
если a≥0, b≥0;
![]()
если a ≤ 0, b≥0
В частности, для квадратных корней:
![]()
если a≥0, b≥0;
![]()
если a ≤ 0, b≥0
Пример. Внести множитель под корень:
![]()
Решение.
![]()
![]()
Ответ:
![]()
Приведение подкоренного выражения к целому виду
Привести подкоренное выражение к целому виду — это значит освободить подкоренное выражение от знаменателя (если он есть):
![]()
Пример 1.
![]()
Ответ:
![]()
Упростить корень — это значит:
1) вынести множитель из-под корня;
2) сократить показатели корня и подкоренного выражения;
3) привести подкоренное выражение к целому виду.
Пример 2. Упростить корень
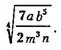
Решение.
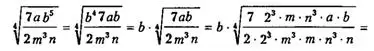
![]()
![]()
Ответ:
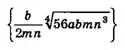
Освобождение дроби от иррациональности в знаменателе дроби или в числителе дроби
Дробь можно освободить от иррациональности (от иррационального выражения) в числителе или в знаменателе, например, так:
![]()
дробь
![]()
освободили от иррациональности в знаменателе;
![]()
дробь
![]()
освободили от иррациональности в числителе.
Чтобы освободить дробь от иррациональности в числителе или в знаменателе, можно применять формулы сокращенного умножения, которые применительно к корням имеют вид:
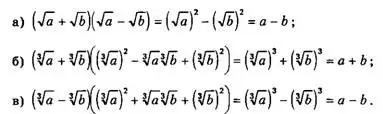
Выражения
![]()
и
![]()
называются взаимно сопряженными выражениями. Их произведение равно разности подкоренных выражений:
![]()
Пример. Освободить дроби от иррациональности в знаменателе:
![]()
Решение.
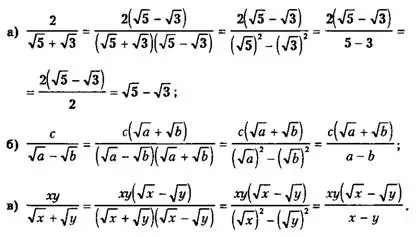
Ответ:
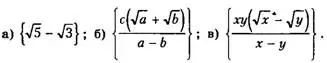
Подобные радикалы
Множитель, стоящий перед корнем, называется его коэффициентом. Например, в выражении
![]()
коэффициентом является число 4. Корни (радикалы) называются подобными, если они имеют одинаковые показатели корней и одинаковые подкоренные выражения, а отличаются только коэффициентом. Например, радикалы
![]()
подобны, т. к.
![]()
![]()






