Периодичность тригонометрических функций. Видеоурок №33

Периодичность тригонометрических функций. Решения упражнений. Учимся решать задачи по тригонометрии. Видеоурок №33
Определение 1. Функция 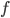$f$ называется периодической, если существует такое число $T\neq 0$ (называемое периодом), что для любого $x$ из области определения этой функции числа $x-T$ и $x+T$ также принадлежат ее области определения, причем $f(x+T)=f(x)$.

Определение 2. Функция 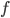$f$ называется периодической, если существует такое число $T\neq 0$, что для любого $x$ из области определения этой функции $f(x)=f(x-T)=f(x+T)$.

Полный урок смотрите в следующем видео:

Домашнее задание:
1. Показать, что число 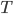$T$ является периодом функции $f$:
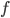1) $\displaystyle f(x)=\sin \frac{x}{2},\; T=4\pi ;$
2) $\displaystyle f(x)=\textrm{tg} \frac{x}{3},\; T=-3\pi ;$
3) $\displaystyle f(x)=\cos 2x,\; T=\pi ;$
4) $\displaystyle f(x)=\textrm{ctg} \pi x,\; T=2 ;$
5) $\displaystyle f(x)=\sin (5x-1),\; T=\frac{4\pi }{5} ;$
6) $\displaystyle f(x)=\cos (3x+2),\; T=-\frac{4\pi }{3} ;$
7) $\displaystyle f(x)=\cos 2\pi x,\; T=3 ;$
8) $\displaystyle f(x)=\sin \frac{\pi x}{2},\; T=8 .$
2. Показать, что число 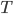$T$ является периодом функции $f$:
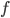1) $\displaystyle f(x)=\cos ^{2}x,\; T=\pi ;$
2) $\displaystyle f(x)=\sin ^{3}x,\; T=-2\pi ;$
3) $\displaystyle f(x)=\left | \sin x \right |,\; T=\pi ;$
4) $\displaystyle f(x)=\left | \textrm{ctg} \frac{x}{2} \right |,\; T=\pi ;$
5) $\displaystyle f(x)=\sin (\cos x),\; T=2\pi ;$
6) $\displaystyle f(x)=\frac{1}{\cos x},\; T=2\pi .$
3. Показать, что число 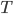$T$ не является периодом функции $f$:
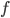1) $\displaystyle f(x)=\sin x,\; T=-\pi ;$
2) $\displaystyle f(x)=\textrm{tg} x,\; T=\frac{\pi }{2} ;$
3) $\displaystyle f(x)=\textrm{ctg} x,\; T=2 .$
4. Доказать, что функция 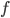$f$ не является периодической:
1) $\displaystyle f=\sqrt{x}-\sqrt{x};$
2) $\displaystyle f=(\sqrt{x-1})^{2}-x;$
3) $\displaystyle f=\cos \sqrt{x}.$