Обратные тригонометрические функции: арксинус, арккосинус, арктангенс, арккотангенс. Видеоурок №34

Обратные тригонометрические функции: арксинус, арккосинус, арктангенс, арккотангенс. Решения упражнений. Учимся решать задачи по тригонометрии. Видеоурок №34
Определение 1. Функция $y=f(x)$ называется обратимой, если для любого $y_{0}\in E(f)$ найдется единственное $x_{0}\in D(f)$ такое, что $y_{0}=f(x_{0})$.
Иначе: функция 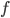$f$ называется обратимой, если она принимает каждое свое значение ровно один раз.
Определение 2. Функция $y=f(x)$ называется обратимой на множестве $M$, если для любых $x_{1}\in M$ и $x_{2}\in M$, $x_{1}\neq x_{2},\; f(x_{1})\neq f(x_{2}).$
Теорема (достаточное условие обратимости). Если функция 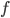$f$ возрастает (убывает) на множестве $M$, то она обратима на этом множестве.

Определение (описательное). Пусть $y=f(x)$ — обратимая функция. Для каждого $x$ из области определения найдем соответствующее значение $y$ функции. Рассмотрим множество упорядоченных пар вида $(x;y)$, т.е. $(x;f(x))$. Множество первых компонентов пар — это область определения функции, множество вторых компонентов — это область значений функции. 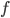Среди этих пар нет таких, у которых равны первые компоненты, потому что $f$ — функция. Среди этих пар нет и таких, у которых равны вторые компоненты, потому что 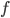$f$ — обратимая функция. Поменяем местами компоненты пар, получим множество пар вида $(y;x)$ с неравными первыми компонентами. Тогда это множество, в свою очередь, задает функцию. Эту функцию будем называть обратной данной. Также вновь построенную функцию и данную будем называть взаимно обратными.
Итак, чтобы из данной обратимой функции 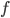$f$ получить обратную ей, надо поменять местами компоненты упорядоченных пар вида $(x;f(x))$.
Теперь становится совершенно очевидно, что если функции 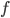$f$ и $g$ взаимно обратны, то $D(f)=E(g)$ и $E(f)=D(g)$, т.е. при переходе от данной функции к обратной области определения и значения меняются местами.
Определение. Функции 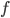$f$ и $g$ называются взаимно обратными, если $D(f)=E(g)$, $E(f)=D(g)$, а также для любого $x\in D(f)\; g(f(x))=x$ и для любого $x\in D(g)\; f(g(x))=x$.
Теорема. Графики взаимно обратных функций симметричны относительно прямой 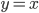$y=x$.

Полный урок смотрите в следующем видео:

Домашнее задание:
1. Докажите, что:
1) $\displaystyle \textrm{arcsin} 0=0;$
2) $\displaystyle \textrm{arcsin} \frac{1}{2}=\frac{\pi }{6};$
3) $\displaystyle \textrm{arcsin} \frac{\sqrt{2}}{2}=\frac{\pi }{4};$
4) $\displaystyle \textrm{arcsin} \frac{\sqrt{3}}{2}=\frac{\pi }{3};$
5) $\displaystyle \textrm{arcsin} \left ( - \frac{1}{2}\right )=-\frac{\pi }{6};$
6) $\displaystyle \textrm{arcsin} (- 1)=-\frac{\pi }{2}.$
2. Является ли верным равенство:
1) $\displaystyle \textrm{arcsin}\pi =0;$
2) $\displaystyle \textrm{arcsin}(-1) =\frac{3\pi }{2};$
3) $\displaystyle \textrm{arcsin} \frac{\pi }{6}=\frac{1}{2};$
4) $\displaystyle \textrm{arcsin}1+ \textrm{arcsin}\left ( -\frac{\sqrt{3}}{2} \right )=\frac{\pi }{6};$
5) $\displaystyle \textrm{arcsin}\frac{1}{2}+ \textrm{arcsin}\left ( -\frac{1}{2} \right )=0;$
6) $\displaystyle \textrm{arcsin}1\cdot \textrm{arcsin}\frac{1}{2} =\frac{\pi ^{2}}{12};$
7) $\displaystyle \left ( \textrm{arcsin}\frac{\sqrt{2}}{2} \right )^{2} =\frac{\pi ^{2}}{16}.$
3. Докажите, что:
1) $\displaystyle \textrm{arccos}0=\frac{\pi }{2};$
2) $\displaystyle \textrm{arccos}\frac{1}{2}=\frac{\pi }{3};$
3) $\displaystyle \textrm{arccos}\frac{\sqrt{2}}{2}=\frac{\pi }{4};$
4) $\displaystyle \textrm{arccos}\frac{\sqrt{3}}{2}=\frac{\pi }{6};$
5) $\displaystyle \textrm{arccos}\left ( -\frac{1}{2} \right )=\frac{2\pi }{3};$
6) $\displaystyle \textrm{arccos} ( -1 )=\pi .$
4. Является ли верным равенство:
1) $\displaystyle \textrm{arccos}\frac{1}{2}=-\frac{\pi }{3};$
2) $\displaystyle \textrm{arccos}0=-\frac{\pi }{2};$
3) $\displaystyle \textrm{arccos}\frac{\pi }{2}=0;$
4) $\displaystyle \textrm{arccos}\frac{2\pi }{3}=-\frac{1}{2};$
5) $\displaystyle \textrm{arccos}\left ( -\frac{\sqrt{2}}{2} \right )+\textrm{arccos}\frac{\sqrt{2}}{2}=\pi;$
6) $\displaystyle \textrm{arccos}\frac{\sqrt{2}}{2}\cdot \textrm{arccos}\left ( -\frac{1}{2} \right )=-\frac{\pi ^{2}}{12};$
7) $\displaystyle \textrm{arccos}^{2}\left ( \frac{-\sqrt{3}}{2} \right )=\frac{25\pi ^{2}}{36}.$
5. Докажите, что:
1) $\displaystyle \textrm{arctg}\frac{\sqrt{3}}{3}=\frac{\pi }{6};$
2) $\displaystyle \textrm{arctg}(-\sqrt{3})=-\frac{\pi }{3};$
3) $\displaystyle \textrm{arctg}1=\frac{\pi }{4};$
4) $\displaystyle \textrm{arcctg}\, 0=\frac{\pi }{2};$
5) $\displaystyle \textrm{arcctg}\sqrt{3}=\frac{\pi }{6};$
6) $\displaystyle \textrm{arcctg}\sqrt{3}=\frac{\pi }{6};$
7) $\displaystyle \textrm{arcctg}\, (-x)=\pi -\textrm{arcctg}\, x;$
8) $\displaystyle \textrm{arctg}\, (-x)= -\textrm{arctg}\, x.$
6. Является ли верным равенство:
1) $\displaystyle \textrm{arctg}\, 0= \pi ;$
2) $\displaystyle \textrm{arctg}\, (-1)=\frac{3\pi }{4} ;$
3) $\displaystyle \textrm{arcctg}\, \frac{\pi }{2}=0 ;$
4) $\displaystyle \textrm{arctg}\, \frac{\pi }{6}=\frac{\sqrt{3}}{3} ;$
5) $\displaystyle \textrm{arctg}\, 1+\textrm{arctg}\, \frac{\sqrt{3}}{3}=\frac{5\pi}{12} ;$
6) $\displaystyle \textrm{arctg}\, \sqrt{3}+\textrm{arcctg}\, (-1)=\frac{\pi}{12} ;$
7) $\displaystyle \textrm{arctg}\, \frac{\sqrt{3}}{3}+\textrm{arcctg}\, \frac{\sqrt{3}}{3}=\frac{\pi}{2}.$