Решение упражнений на обратные тригонометрические функции. Видеоурок №35

Обратные тригонометрические функции: арксинус, арккосинус, арктангенс, арккотангенс. Решения упражнений. Учимся решать задачи по тригонометрии. Видеоурок №35
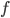Определение (описательное). Функция $f(x)=\sin x$ обратимой не является. Рассмотрим эту функцию на искусственной области определения $\displaystyle D(f)=\left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]$. На этом множестве функция $f$ — возрастающая, следовательно, обратимая. Функция, обратная функции $\displaystyle f(x)=\sin x,\; D(f)=\left [ -\frac{\pi }{2};\frac{\pi }{2} \right ],$ называется арксинусом и обозначается $g(x)=\textrm{arcsin}\, x$.
Итак, $g(x)=\textrm{arcsin}\, x$ — это функция, обратная функции $f(x)=\sin x$ на промежутке $\displaystyle \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]$.
Определение. Арксинусом числа $a$ называется такое число $b$ из отрезка $\displaystyle \left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]$, синус которого равен $a$.

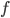Определение (описательное). Функция $f(x)=\cos x$ обратимой не является. Рассмотрим эту функцию на искусственной области определения $D(f)=\left [ 0;\pi \right ]$. На этом интервале функция $f$ — убывающая, а следовательно, обратима. Функция, обратная функции $f(x)=\cos x;\: D(f)=\left [ 0;\pi \right ]$, называется арккосинусом и обозначается $g(x)=\textrm{arccos}\, x$.

Итак, $g(x)=\textrm{arccos}\, x$ — это функция, обратная функции $f(x)=\cos x$ на промежутке $\left [ 0;\pi \right ]$.
Определение. Арккосинусом числа $a$ называется такое число $b$ из отрезка $\left [ 0;\pi \right ]$, косинус которого равен $a$.

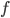Определение (описательное). Функция $f(x)=\textrm{tg}\, x$ обратимой не является. Рассмотрим эту функцию на искусственной области определения $\displaystyle D(f)=\left ( -\frac{\pi }{2};\frac{\pi }{2} \right )$. На этом множестве функция $f$ возрастает, а следовательно, обратима. Функция, обратная функции $f(x)=\textrm{tg}\, x$, $\displaystyle D(f)=\left ( -\frac{\pi }{2};\frac{\pi }{2} \right )$, называется арктангенсом и обозначается $g(x)=\textrm{arctg}\, x$.
Итак, $g(x)=\textrm{arctg}\, x$ — это функция, обратная функции $f(x)=\textrm{tg}\, x$ на промежутке $\displaystyle D(f)=\left ( -\frac{\pi }{2};\frac{\pi }{2} \right )$.

Определение. Арктангенсом числа $a$ называется такое число $b$ из промежутка $\displaystyle \left ( -\frac{\pi }{2};\frac{\pi }{2} \right )$, тангенс которого равен $a$.

Определение. Функция, обратная функции $f(x)=\textrm{ctg}\, x,\; D(f)=(0;\pi )$, называется арккотангенсом и обозначается $g(x)=\textrm{arcctg}\, x$.

Полный урок смотрите в следующем видео:

Домашнее задание:
1. Вычислить:
1) $\displaystyle \textrm{tg}(\arccos \frac{\sqrt{2}}{2});$
2) $\displaystyle \textrm{ctg}(\arcsin \frac{\sqrt{3}}{2});$
3) $\displaystyle \sin \left ( \arccos \frac{1}{2} \right );$
4) $\displaystyle \cos (2 \textrm{arctg} 1);$
5) $\displaystyle \cos \left ( 2 \arccos\frac{\sqrt{3}}{2} \right );$
6) $\displaystyle \cos \left ( \frac{1}{2} \arcsin\frac{\sqrt{3}}{2} \right );$
7) $\displaystyle \textrm{ctg} \left ( 2 \arcsin\frac{1}{\sqrt{2}} \right );$
8) $\displaystyle \textrm{ctg} \left ( 2 \textrm{arcctg}(-\sqrt{3}) \right );$
9) $\displaystyle \sin \left ( 3\arcsin \left ( -\frac{\sqrt{3}}{2} \right ) \right );$
10) $\displaystyle \cos \left ( \arccos \left ( -\frac{1}{2} \right )+\frac{\pi }{3} \right );$
11) $\displaystyle \textrm{tg}\left ( 2 \textrm{arctg}\left ( -\frac{1}{\sqrt{3}} \right )+\frac{\pi }{6} \right );$
12) $\displaystyle \cos \left ( 3\arcsin \frac{\sqrt{3}}{2}+\arccos \left ( -\frac{1}{2} \right ) \right ).$
2. Найти область определения функции:
1) $y=\arcsin (x-1);$
2) $\displaystyle y=\arcsin \left ( x+\frac{\pi }{2} \right );$
3) $\displaystyle y=\arcsin \frac{1}{2x};$
4) $\displaystyle y=\arcsin \sqrt{2-x};$
5) $\displaystyle y=\arccos (x+2);$
6) $\displaystyle y=\arccos \frac{2}{3x};$
7) $\displaystyle y=\arccos \sqrt{3-x};$
8) $\displaystyle y=\textrm{arctg} (4-x);$
9) $\displaystyle y=\textrm{arctg} \frac{\pi }{x+5};$
10) $\displaystyle y=\textrm{arctg} \sqrt{x-3};$
11) $\displaystyle y=\textrm{arcctg} \sqrt{x+2};$
12) $\displaystyle y=\textrm{arcctg} \frac{\pi }{x+7}.$
3. Найти область значений функции:
1) $\displaystyle y=\arcsin x+\frac{\pi }{2};$
2) $\displaystyle y=\arccos x+2;$
3) $\displaystyle y=\arcsin \sqrt{x}+4;$
4) $\displaystyle y=\arccos \sqrt{-x}+2;$
5) $\displaystyle y=\sqrt{\arcsin x};$
6) $\displaystyle y=\frac{1}{\arcsin x};$
7) $\displaystyle y=\frac{1}{\arccos x};$
8) $\displaystyle y=\textrm{arctg}x+2;$
9) $\displaystyle y=\textrm{arcctg}x+4;$
10) $\displaystyle y=\frac{1}{\textrm{arctg}x};$
11) $\displaystyle y=\frac{1}{\textrm{arcctg}x}.$