Построение графиков тригонометрических функций с помощью преобразований. Видеоурок №41

Построение графиков тригонометрических функций с помощью преобразований. Решения упражнений. Учимся решать задачи по тригонометрии. Видеоурок №41

Пример 1. Построить график функции $\displaystyle y=\frac{1}{\sin x}$.
Решение.
Прежде всего заметим, что эта функция периодическая с периодом $2\pi$. Поэтому будем строить ее график на отрезке $[0;2\pi )$ длиной в период. Понятно, что построение будем вести с помощью графика $y=\sin x$. Обратим внимание, что значения функций $y=\sin x$ и $\displaystyle y=\frac{1}{\sin x}$ в точках $\displaystyle x=\frac{\pi }{2}+\pi k,\; k\in \mathbb{Z}$, совпадают на рассматриваемом промежутке $[0;2\pi )$ это будут точки $\displaystyle \frac{\pi }{2}$ и $\displaystyle \frac{3\pi }{2}$. Если $x\in [0;\pi ]$, причем $x \to 0$ или $x \to 2\pi$, то $\displaystyle \frac{1}{\sin x} \to +\infty$. Если $x\in [\pi ;2\pi ]$, причем $x \to \pi$ или $x \to 2\pi$, то $\displaystyle \frac{1}{\sin x} \to -\infty$.

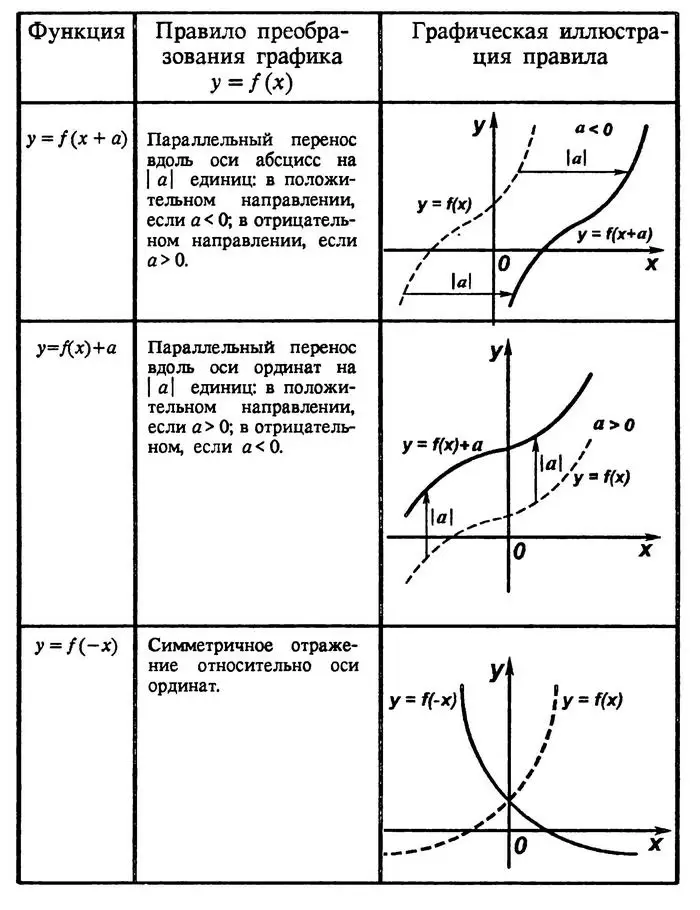
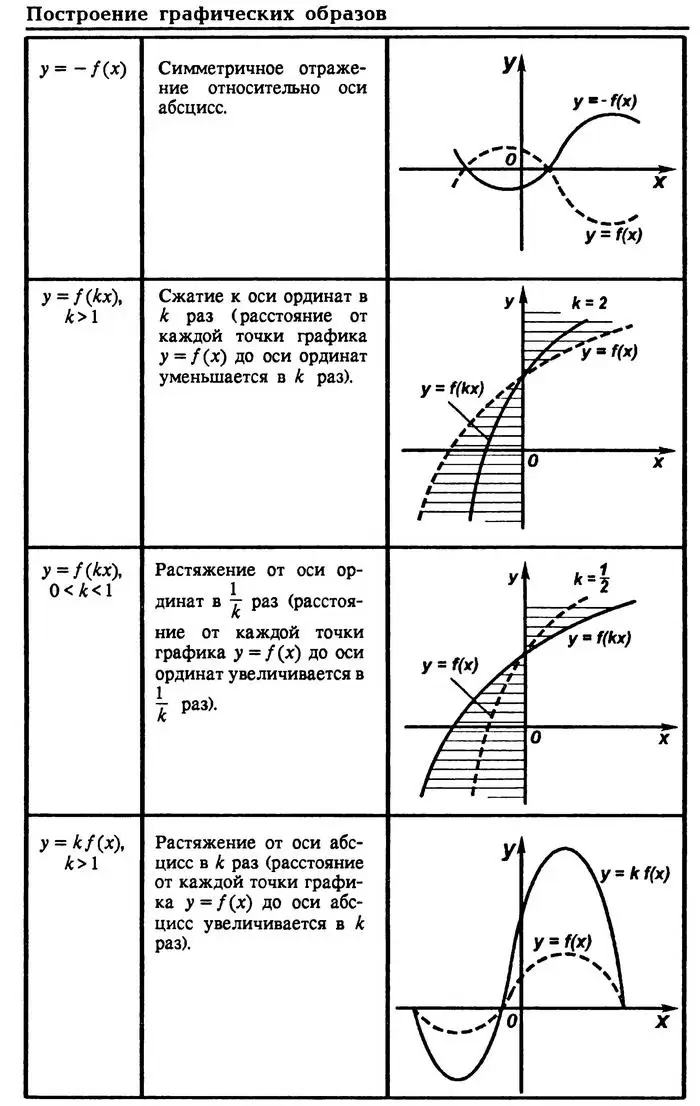
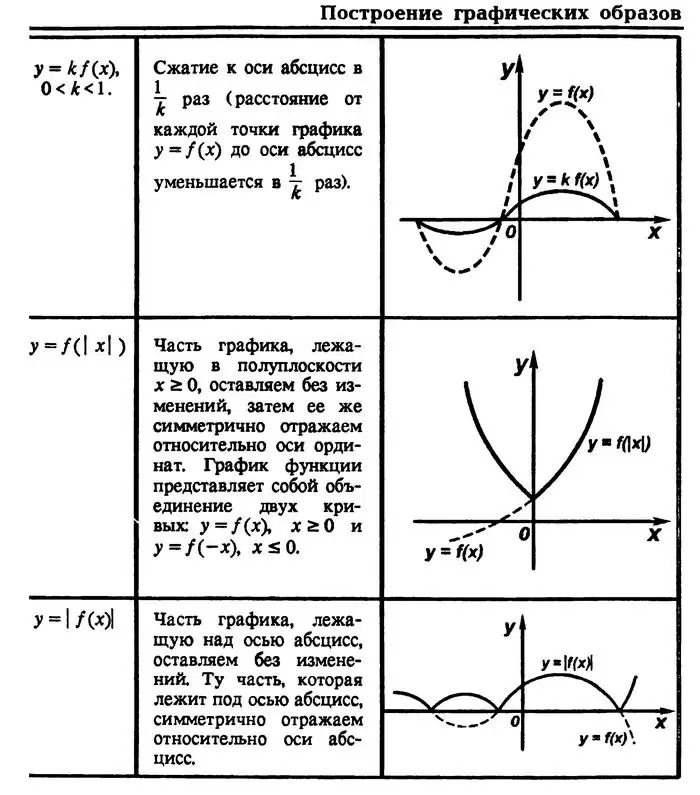
Полный урок смотрите в следующем видео:

Домашнее задание:
1. Постройте график функции:
1) $\displaystyle y=\frac{1}{\cos x};$
2) $\displaystyle y=\frac{1}{\arcsin x};$
3) $\displaystyle y=\frac{1}{\arccos x};$
2. Постройте график функции:
1) $\displaystyle y=2\cos ^{2}\frac{x}{2};$
2) $\displaystyle y=2\sin ^{2}\frac{x}{2};$
3) $\displaystyle y=\cos ^{2}x;$
4) $\displaystyle y=\sin ^{2}x;$
5) $\displaystyle y=\sin ^{2}x-\cos 2x;$
6) $\displaystyle y=\sin x-\cos x.$
3. Постройте график функции:
1) $\displaystyle y=(\sqrt{\sin x})^{2};$
2) $\displaystyle y=(\sqrt{\cos x})^{2};$
3) $\displaystyle y=\sqrt{1-\sin^{2}x};$
4) $\displaystyle y=\sqrt{1-\cos^{2}x};$
5) $\displaystyle y=\sqrt{\frac{1-\cos x}{2}}.$