Решение тригонометрических уравнений с помощью введения вспомогательного угла. Видеоурок №49

Тригонометрические уравнения, при решении которых используются формулы тройного аргумента. Уравнения, которые решают с помощью умножения на некоторую тригонометрическую функцию. Как решать тригонометрические уравнения. Учимся решать задачи по тригонометрии. Видеоурок №49
При решении уравнений иногда требуется умножить обе его части на выражение с переменной (обозначим его $f(x)$). Ясно, что такое преобразование не всегда является тождественным. Если область определения $f(x)$ уже области определения уравнения, то возможна потеря корней. Если же область определения $f(x)$ шире области определения уравнения, или они совпадают, то возможно приобретение посторонних корней за счет корней уравнения $f(x)=0$. 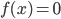Рассмотрим примеры.

Полный урок смотрите в следующем видео:

Домашнее задание:
1. Решить уравнение:
1) $\displaystyle \sin 15x+\sqrt{3}\cos 15x-2=0;$
2) $\displaystyle \sqrt{2}\sin 2x-\sqrt{2}\cos 2x-\sqrt{3}=0;$
3) $\displaystyle \sin 3x-\cos 3x=\sqrt{\frac{3}{2}};$
4) $\displaystyle \sin 5x+\cos 5x=\sqrt{2}\cos 13x;$
5) $\displaystyle 2\cos 41x=\sqrt{2}(\cos 11x-\sin 11x);$
6) $\displaystyle \sqrt{3}(2-\cos x)+4\sin 2x=\sin x.$
2. Решить уравнение:
1) $\displaystyle 3\sin x+4\cos x=2;$
2) $\displaystyle 5\sin x-12\cos x=13;$
3) $\displaystyle 2\sin \frac{x}{2}-3\cos \frac{x}{2}=0,8;$
4) $\displaystyle 3\sin 3x+5\cos 3x=4.$
3. Решить уравнение:
1) $\displaystyle \cos x\cos 2x\cos 4x\cos 8x=\frac{1}{16};$
2) $\displaystyle \cos x\cos 2x\cos 4x\cos 8x=\frac{1}{8}\cos 15x;$
3) $\displaystyle \cos x\cos 2x\cos 3x=0,5\sin ^{2}x-0,25;$
4) $\displaystyle \cos x+\cos 2x+\cos 3x+\cos 4x=-0,5.$