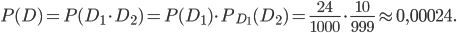Задача №1. Отдел технического контроля фабрики проверяет половину изделий некоторой партии (для проверки изделия из партии берут наудачу) и признает годной всю партию, если среди проверенных изделий будет не более одного бракованного. Какова вероятность того, что плутая из 20 изделий, в которой имеется 2 бракованных, будет признана годной?
Решение. Испытание состоит в проверке качества одного изделия. По условию партия из 20 изделий будет признана годной, если среди проверенных 10 изделий будет не более одного бракованного. Это означает, что годной признается такая партия из 20 изделий, в которой среди проверенных 10 изделий или не будет ни одного бракованного, или же будет одно бракованное.
Рассмотрим события:
 - среди проверенных 10 изделий нет ни одного бракованного;
- среди проверенных 10 изделий нет ни одного бракованного;
 - среди проверенных 10 изделий одно бракованное;
- среди проверенных 10 изделий одно бракованное;
 - среди проверенных 10 изделий не более одного бракованного.
- среди проверенных 10 изделий не более одного бракованного.
 и
и  - несовместные события. Событие
- несовместные события. Событие  представляет собой сумму этих событий:
представляет собой сумму этих событий: 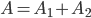 .
.
Вероятность события  найдем по теореме сложения вероятностей несовместных событий. По формуле (1) получим
найдем по теореме сложения вероятностей несовместных событий. По формуле (1) получим
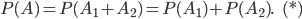
Вероятности
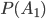 и
и 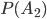 найдем, воспользовавшись классическим определением вероятности. Событие
найдем, воспользовавшись классическим определением вероятности. Событие  состоит в том, что все 10 проверенных изделий являются годными. Общее число исходов испытания для события
состоит в том, что все 10 проверенных изделий являются годными. Общее число исходов испытания для события  равно
равно 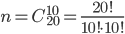 .
.Для наступления события
 должны быть взяты 10 годных из 18-и годных изделий, имеющихся во всей партии, причем порядок, в котором они будут взяты, роли не играет. Следовательно, число исходов испытания, благоприятствующих событию
должны быть взяты 10 годных из 18-и годных изделий, имеющихся во всей партии, причем порядок, в котором они будут взяты, роли не играет. Следовательно, число исходов испытания, благоприятствующих событию  , равно
, равно 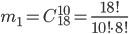 . Согласно формуле (1) получим
. Согласно формуле (1) получим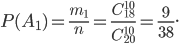
Событие
 состоит в том, что среди 10 проверенных изделий есть одно бракованное, а остальные 9 - годные. Число исходов испытания, благоприятствующих событию
состоит в том, что среди 10 проверенных изделий есть одно бракованное, а остальные 9 - годные. Число исходов испытания, благоприятствующих событию  равно
равно 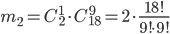 . Общее число исходов испытания для события
. Общее число исходов испытания для события  равно
равно 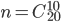 . Применив формулу (1), получим
. Применив формулу (1), получим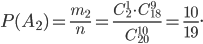
Подставив значения
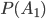 и
и 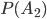 в равенство (*), найдем
в равенство (*), найдем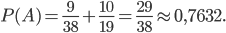
Задача №2. В круг радиуса
 вписан равносторонний треугольник. Какова вдюятность того, что четыре наугад поставленные в данном круге точки окажутся внутри треугольника?
вписан равносторонний треугольник. Какова вдюятность того, что четыре наугад поставленные в данном круге точки окажутся внутри треугольника?Решение. Рассмотрим события:
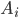 - наугад поставленная в круг точка окажется внутри вписанного в этот круг равностороннего треугольника (і=1,2,3,4).
- наугад поставленная в круг точка окажется внутри вписанного в этот круг равностороннего треугольника (і=1,2,3,4). - четыре наугад поставленные в круг точки окажутся внутри вписанного в этот круг равностороннего треугольника.
- четыре наугад поставленные в круг точки окажутся внутри вписанного в этот круг равностороннего треугольника.Событие
 состоит в том, что внутри треугольника окажутся и первая, и вторая, и третья, и четвертая точки. Это означает, что событие
состоит в том, что внутри треугольника окажутся и первая, и вторая, и третья, и четвертая точки. Это означает, что событие  представляет собой произведение событий
представляет собой произведение событий 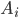 :
: 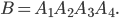
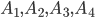 - независимые события, имеющие равные веpoятнoсти. Обозначим:
- независимые события, имеющие равные веpoятнoсти. Обозначим: 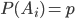 . Вероятность
. Вероятность 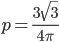 (см. геометрические вероятности).
(см. геометрические вероятности).Вероятность события
 найдем по теореме умножения вероятностей независимых событий. Применив формулу (8), получим
найдем по теореме умножения вероятностей независимых событий. Применив формулу (8), получим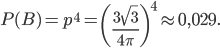
Задача №3. В некоторой серии денежно-вещевой лотереи на 1000 билетов приходится 24 денежных и 10 вещевых выигрышей. Некто приобрел 2 билета этой серии. Какова вероятностъ выигрыша:
а) хотя бы по одному билету;
б) по первому билету денег, а по второму - вещи?
Решение.
а) Обозначим событие:
 - выигрыш хотя бы по одному из двух билетов лотереи.
- выигрыш хотя бы по одному из двух билетов лотереи.Найдем вероятность события
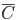 , противоположного событию
, противоположного событию  . Рассмотрим события:
. Рассмотрим события: - проигрыш по первому билету;
- проигрыш по первому билету; - проигрыш по второму билету;
- проигрыш по второму билету; - проигрыш по двум билетам.
- проигрыш по двум билетам.Событие
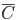 состоит в том, что выигрыш не выпадет ни на первый, ни на второй билеты. Это означает, что событие
состоит в том, что выигрыш не выпадет ни на первый, ни на второй билеты. Это означает, что событие  представляет собой произведение событий
представляет собой произведение событий  и
и  ,
, 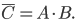
В лотерее на 1000 билетов приходится 34 выигрышных, остальные 966 - проигрышные. Воспользовавшись классическим определением вероятности, получим, что вероятность события
 равна
равна 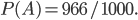
Наступление события
 изменяет вероятность события
изменяет вероятность события  . Это означает, что событие
. Это означает, что событие  является зависимым от события
является зависимым от события  , Условная вероятность
, Условная вероятность 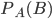 =965/999.
=965/999.Вероятность события
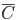 найдем по теореме умножения вероятностей зависимых событий. По формуле (5) получим
найдем по теореме умножения вероятностей зависимых событий. По формуле (5) получим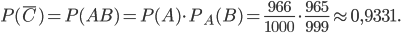
Искомую вероятностъ
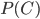 найдем, воспользовавшись формулой (4):
найдем, воспользовавшись формулой (4): 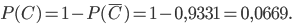
б) Рассмотрим события:
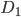 - денежный выигрыш по первому билету;
- денежный выигрыш по первому билету;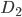 - вещевой выигрыш по второму билету;
- вещевой выигрыш по второму билету;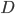 - выигрыш по первому билету денег, а по второму - вещи.
- выигрыш по первому билету денег, а по второму - вещи.Событие
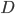 представляет собой произведение событий
представляет собой произведение событий 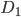 и
и 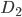 :
: 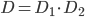 .
.Вероятность события
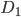 найдем, воспользовавшись формулой (1):
найдем, воспользовавшись формулой (1):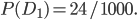 Наступление события
Наступление события 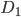 изменяет вероятность события
изменяет вероятность события 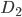 (при наступлении события
(при наступлении события 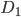 общее число исходов испытания уменьшается на 1). Это означает, что
общее число исходов испытания уменьшается на 1). Это означает, что 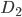 - событие, зависимое от события
- событие, зависимое от события 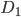 . Условная вероятность
. Условная вероятность 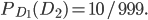 Вероятность события
Вероятность события 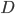 найдем по теореме умножения вероятностей зависимых событий. Применив формулу (5), получим
найдем по теореме умножения вероятностей зависимых событий. Применив формулу (5), получим