Формулы двойного и тройного аргументов. Видеоурок №19

Формулы двойного и тройного аргументов. Решения упражнений. Учимся решать задачи по тригонометрии. Видеоурок №19

Формулы двойного и тройного углов

$$\displaystyle \begin{matrix} \sin 2\alpha =2\sin \alpha \cos \alpha ;\\ \cos 2\alpha =\cos ^{2}\alpha -\sin ^{2}\alpha =2\cos ^{2}\alpha-1=1-2 \sin ^{2}\alpha;\\ \textrm{tg}2\alpha =\frac{2\textrm{tg}\alpha}{1-\textrm{tg}^{2}\alpha};\\ \sin 3\alpha =3\sin \alpha -4\sin ^{3}\alpha ;\\ \cos 3\alpha =4\cos ^{3}\alpha -3\cos \alpha ;\\ \textrm{tg}3\alpha =\frac{3\textrm{tg}\alpha -\textrm{tg}^{3}\alpha }{1-3\textrm{tg}^{2}\alpha }. \end{matrix}$$

Полный урок смотрите в следующем видео:

Домашнее задание:
1. Упростить выражение:

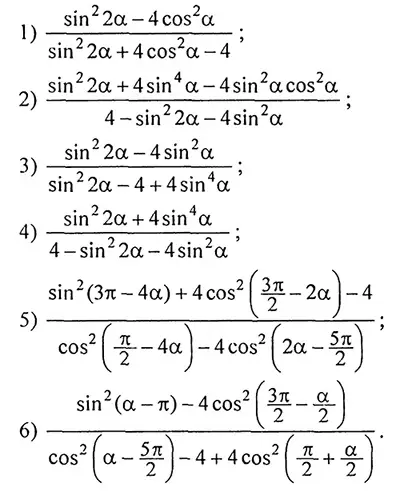
2. Доказать тождество:

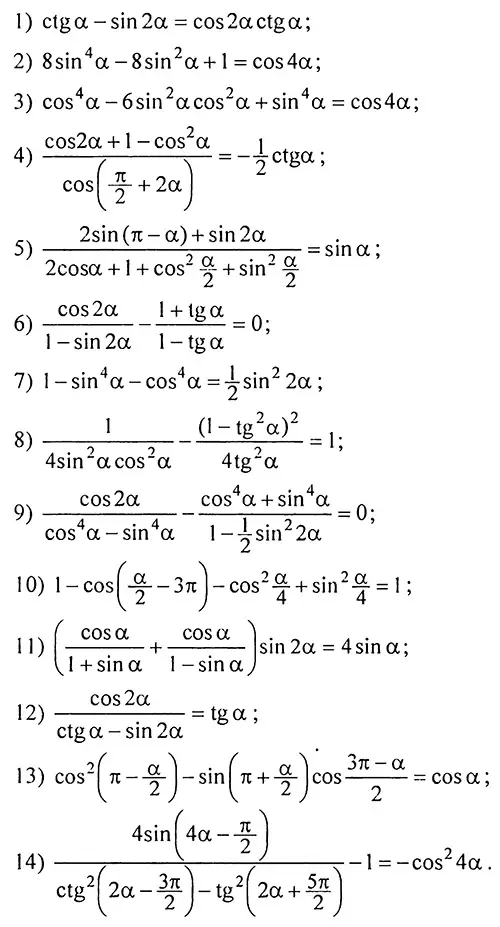
3. Упростить выражение:

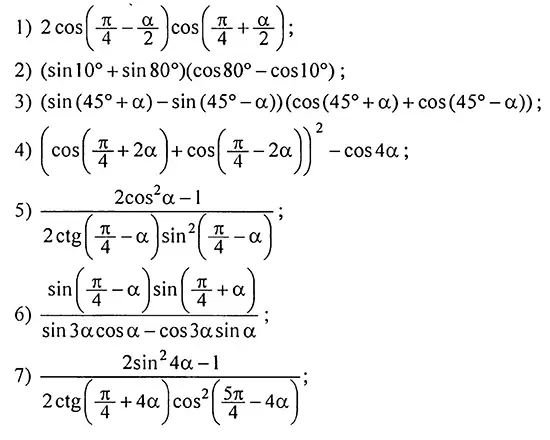
4. Доказать тождество:

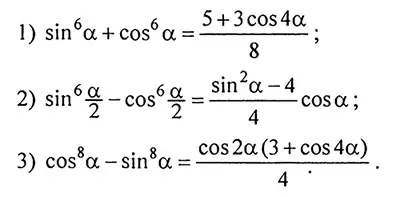
5. Упростить выражение:
1) $\displaystyle \sqrt{(\textrm{ctg}^{2}\alpha -\textrm{tg}^{2}\alpha)}\cdot \textrm{tg}2\alpha,$ если $\displaystyle \frac{\pi }{4}<\alpha <\frac{\pi }{2}$;

2) $\displaystyle \sqrt{(\textrm{ctg}\alpha -\textrm{tg}\alpha)2\textrm{ctg}2\alpha}\cdot \textrm{tg}2\alpha+2,$ если $\displaystyle \frac{\pi }{2}<\alpha <\frac{3\pi }{4}$;

3) $\displaystyle \sqrt{\left ( 1-\textrm{tg}^{2}\frac{\alpha }{2} \right )\left ( \textrm{ctg}^{2}\frac{\alpha }{2}-1 \right )}$, если $\displaystyle \pi <\alpha <\frac{3\pi }{2}$.

6. Дано: $\displaystyle \sin \alpha =0,96,\: 0^{\circ}<\alpha <90^{\circ}$. Найти $\displaystyle \sin 2\alpha ,\cos 2\alpha ,\textrm{tg}2\alpha$.

7. Дано: $\displaystyle \textrm{tg}\alpha =-2,4,\: 90^{\circ}<\alpha <180^{\circ}$. Найти $\displaystyle \sin 2\alpha ,\cos 2\alpha$.

8. Дано: $\displaystyle \textrm{tg}\alpha =-2.$ Найти $\displaystyle \textrm{tg}2\alpha,\: \textrm{tg}4\alpha$.

9. Дано: $\displaystyle \textrm{tg}\frac{\varphi }{6}=0,5$. Найти $\displaystyle \textrm{tg}\left ( 45^{\circ}-\frac{\varphi }{3} \right )$.

10. Дано: $\displaystyle \cos \frac{\alpha }{2}=0,1$. Найти $\displaystyle \cos \alpha$.

11. Дано: $\displaystyle \sin \frac{\alpha }{2}=\frac{3}{5},\: \frac{\pi }{2}<\alpha <\pi$. Найти $\displaystyle \sin \alpha ,\cos \alpha ,\textrm{tg}\alpha$.