Формулы приведения. Решения упражнений. Видеоурок №13

Формулы приведения. Решения упражнений. Учимся решать задачи по тригонометрии. Видеоурок №13
Обратим внимание на закономерности в формулах приведения: функция в правой части равенства берется с тем же знаком, какой имеет исходная функция, если считать, что угол $\alpha$ является углом I четверти; для углов $\pi \pm \alpha ,\: 2\pi \pm \alpha ,\: 3\pi \pm \alpha ,...$ название исходной функции сохраняется; для углов $\displaystyle \frac{\pi}{2} \pm \alpha ,\: \frac{3\pi}{2} \pm \alpha ,\: \frac{5\pi}{2} \pm \alpha ,...$ название исходной функции заменяется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс). 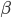В частности, если $\alpha$ и $\beta$ такие, что $\displaystyle \alpha +\beta =\frac{\pi }{2}$, то $\displaystyle \sin \alpha =\cos \beta, \: \textrm{tg}\alpha =\textrm{ctg}\beta$.

Полный урок смотрите в следующем видео:

Домашнее задание:
1. Привести к тригонометрической функции угла $\alpha$:
1) $\displaystyle \sin \left ( \frac{\pi }{2}-\alpha \right );$
2) $\displaystyle \cos \left ( \frac{3\pi }{2}+\alpha \right );$
3) $\displaystyle \textrm{tg} \left ( \frac{3\pi }{2}-\alpha \right );$
4) $\displaystyle \textrm{ctg} \left ( \frac{3\pi }{2}-\alpha \right );$
5) $\displaystyle \sin \left ( \pi-\alpha \right );$
6) $\displaystyle \cos \left ( \pi-\alpha \right );$
7) $\displaystyle \textrm{tg} (180^{\circ}+\alpha );$
8) $\displaystyle \textrm{ctg} (270^{\circ}-\alpha );$
9) $\displaystyle \sin (360^{\circ}+\alpha );$
10) $\displaystyle \cos (360^{\circ}+\alpha );$
11) $\displaystyle \textrm{tg} (\alpha -360^{\circ});$
12) $\displaystyle \textrm{ctg} (\alpha -270^{\circ});$
13) $\displaystyle \cos (-\alpha+270^{\circ});$
14) $\displaystyle \sin (180^{\circ}+\alpha );$
15) $\displaystyle \cos (\alpha -180^{\circ});$
16) $\displaystyle \sin^{2} \left ( \frac{5\pi }{2}+\alpha \right );$
17) $\displaystyle \cos ^{2}(3\pi -\alpha );$
18) $\displaystyle \textrm{tg}^{4}\left ( \alpha -\frac{9\pi }{2} \right );$
19) $\displaystyle \textrm{ctg}^{2}(90^{\circ}+\alpha );$
20) $\displaystyle \cos \left ( \frac{\pi }{2}+\alpha \right );$
21) $\displaystyle \sin \left ( \frac{3\pi }{2}-\alpha \right ).$

2. Привести к значению тригонометрической функции наименьшего положительного аргумента:
1) $\cos 123^{\circ};$
2) $\textrm{tg} 174^{\circ};$
3) $\sin 216^{\circ};$
4) $\textrm{ctg} 194^{\circ};$
5) $\cos (-218^{\circ});$
6) $\sin (-317^{\circ});$
7) $\cos 400^{\circ};$
8) $\textrm{ctg}(-0,7\pi );$
9) $\cos \frac{5\pi }{9}.$

3. Вычислить:
1) $\textrm{ctg}(-330^{\circ});$
2) $\cos 225^{\circ};$
3) $\textrm{tg}(-240^{\circ});$
4) $\cos (-150^{\circ});$
5) $\textrm{ctg} 300^{\circ};$
6) $\sin 240^{\circ};$
7) $\textrm{tg} 210^{\circ};$
8) $\textrm{ctg} 315^{\circ};$
9) $\textrm{tg}\frac{7\pi }{4};$
10) $\cos \frac{5\pi }{4};$
11) $\textrm{ctg}\frac{11\pi }{6};$
12) $\cos \frac{13\pi }{6};$
13) $\cos \left ( -\frac{4\pi }{3} \right );$
14) $\sin \left ( -\frac{5\pi }{3} \right );$
15) $\cos 10\pi ;$
16) $\sin 7\pi ;$
17) $\sin 1110^{\circ};$
18) $\textrm{ctg}(-1200^{\circ}).$