Сравнение значений тригонометрических функций. Видеоурок №7

Сравнение значений тригонометрических функций. Учимся решать задачи по тригонометрии. Видеоурок №7
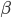Свойство. Если $\alpha$ и $\beta$ - углы одной четверти и

Полный урок смотрите в следующем видео:

Домашнее задание:
1. Сравните:
1) $\cos 1,6\pi$ и $\cos 1,68\pi$;
2) $\textrm{tg} 7,2\pi$ и $\textrm{tg} 7,25\pi$;
3) $\sin 20^{\circ}$ и $\sin 21^{\circ}$;
4) $\cos 20^{\circ}$ и $\cos 21^{\circ}$;
5) $\sin 200^{\circ}$ и $\sin 250^{\circ}$;
6) $\cos 200^{\circ}$ и $\cos 250^{\circ}$;
7) $\textrm{ctg} 200^{\circ}$ и $\textrm{ctg} 250^{\circ}$;
8) $\cos 5,1$ и $\cos 5$;
9) $\sin 2$ и $\sin 2,1$;
10) $\textrm{ctg} 6$ и $\textrm{ctg} 6,2$.
2. Сравните:
1) $\sin 58^{\circ}$ и $\cos 58^{\circ}$;
2) $\sin 18^{\circ}$ и $\cos 18^{\circ}$;
3) $\sin 81^{\circ}$ и $\cos 81^{\circ}$;
4) $\sin 20^{\circ}$ и $\cos 20^{\circ}$;
5) $\sin 40^{\circ}$ и $\textrm{ctg} 20^{\circ}$;
6) $\cos 80^{\circ}$ и $\sin 70^{\circ}$.
3. Возможно ли равенство:
1) $\cos \alpha =2\sin 20^{\circ};$
2) $\displaystyle \sin \alpha =\frac{2}{3}\textrm{tg}80^{\circ};$
3) $\displaystyle \cos \alpha =\textrm{ctg}10^{\circ};$
4) $\sin \alpha =\textrm{tg}\frac{\pi }{9}$.