Тригонометрические функции числового аргумента. Учимся решать задачи по тригонометрии. Видеоурок №2
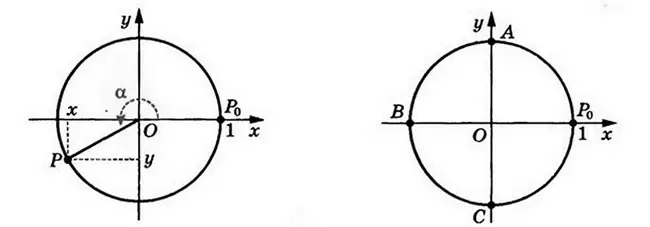
Косинусом и синусом угла поворота  называют соответственно абсциссу
называют соответственно абсциссу  и ординату
и ординату  точки
точки  единичной окружности, полученной в результате поворота точки
единичной окружности, полученной в результате поворота точки  около начала координат на угол
около начала координат на угол  .
.
Точки  на рисунке справа имеют соответственно координаты (1;0), (0;1), (-1;0), (0;-1). Они получены из точки
на рисунке справа имеют соответственно координаты (1;0), (0;1), (-1;0), (0;-1). Они получены из точки  в результате поворота соответственно на такие углы:
в результате поворота соответственно на такие углы:  .
.
Тангенсом угла поворота  называется отношение синуса этого угла к его косинусу:
называется отношение синуса этого угла к его косинусу:  .
.
Котангенсом угла поворота  называется отношение косинуса этого угла к его синусу:
называется отношение косинуса этого угла к его синусу:  .
.
Схемы для определения значений тригонометрических функций
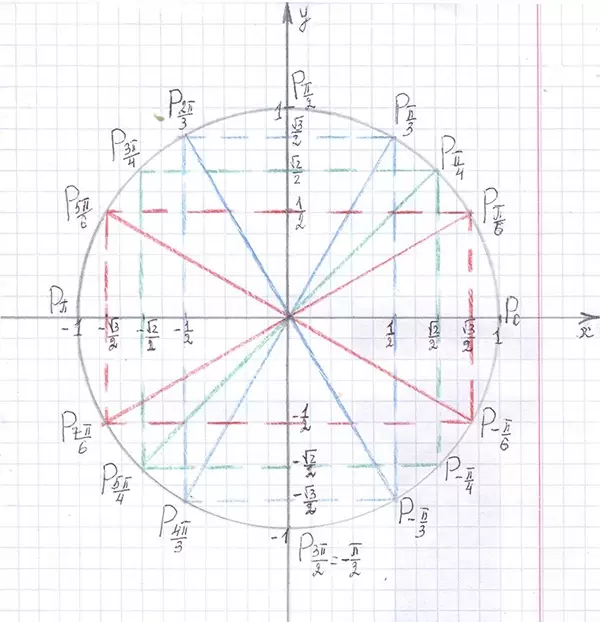
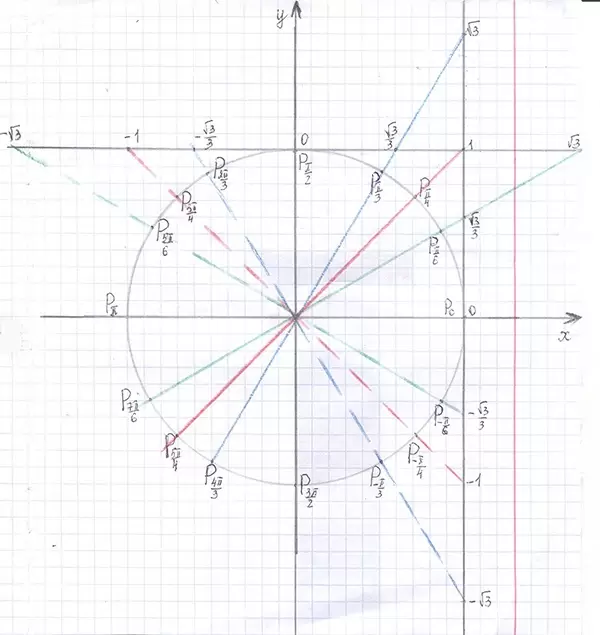
Таблица значений тригонометрических функций
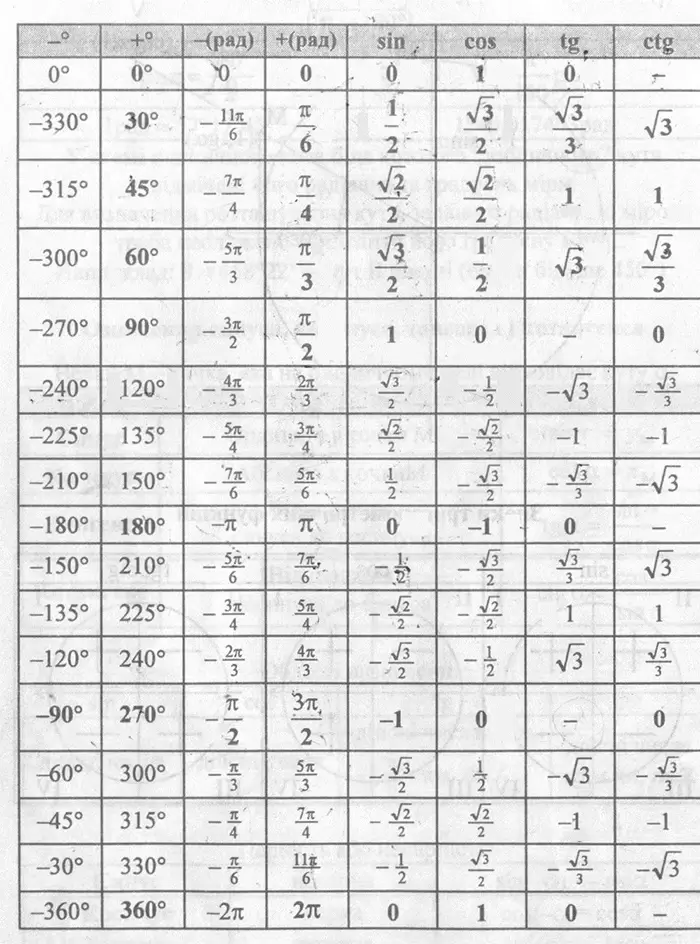
Полный урок смотрите в следующем видео:
Домашнее задание:
Найдите значения функций:

Ответы проверьте по таблице значений тригонометрических функций (см. выше).







